Já falamos que os p-valores não podem ser interpretados como uma medida absoluta de evidência, como comumente costumam ser. Entre algumas interpretações recorrentes, por exemplo, vale mencionar alguns cuidados:
- se para um certo conjunto de dados, uma hipótese A (e uma estatística calculada sob A) gera um p-valor de 1% e outra hipótese B (e uma estatística calculada sob B) gera um p-valor de 10%, isto não necessariamente quer dizer que os dados trazem mais evidência contra A do que contra B. Até porque rejeitar A pode implicar, logicamente, na rejeição de B.
- se para um certo conjunto de dados, uma hipótese A (e uma estatística calculada sob A) gera um p-valor menor que 5%, isto não necessariamente é evidência contra A.
- se um estudo sobre a hipótese A resulta em p-valor menor do que 5% e outro estudo gera um p-valor maior do que 5%, isto não necessariamente quer dizer que os estudos apresentam resultados contraditórios.
Dentre outras questões.
Mas o que essas coisas querem realmente dizer? Muitas vezes é difícil entender o conceito sem exemplos (e gráficos) e é isso que pretendemos trazer hoje aqui. Vamos tratar do primeiro ponto listado, uma questão que, muitas vezes, pode confundir o usuário do p-valor: o p-valor pode apresentar evidências de que alguém seja obeso e, ao mesmo tempo, evidências de que este alguém não seja gordo, caso você, por descuido, tome o p-valor como uma medida absoluta de evidência e leve suas hipóteses nulas ao pé da letra. O exemplo abaixo foi retirado do artigo do Alexandre Patriota (versão publicada aqui).
Considere duas amostras aleatórias, com 100 observações cada, de distribuição normal com médias desconhecidas e variância igual 1. Suponha que as médias amostrais calculadas nas duas amostras tenham sido x1=0.14 e x2=-0.16 e que você queira testar a hipótese nula de que ambas as médias populacionais sejam iguais a zero.
A estatística para esta hipótese é n*(x1^2+x2^2), e o valor obtido na amostra é 100*(0.14^2+(-0.16)^2)=4.52. A distribuição desta estatística, sob a hipótese nula, é uma qui-quadrado com 2 graus de liberdade, o que te dá um p-valor de 10%. Assim, se você segue o padrão da literatura aplicada, como o p-valor é maior do que 5%, você dirá que aceita (ou que não rejeita) a hipótese nula de que as médias sejam iguais a zero.
Agora suponha que outro pesquisador teste, com os mesmos dados, a hipótese de que as médias populacionas sejam iguais a si. Para esta hipótese, a estatística seria (n/2)*(x1 – x2)^2, e o valor obtido na amostra é (100/2)*(0.14+0.16)^2= 4.5. A distribuição desta estatística sob a hipótese nula é uma qui-quadrado com 1 grau de liberdade, o que te dá um p-valor de 3%. Caso o pesquisador siga o padrão da literatura aplicada, como o p-valor é menor do que 5% (o tão esperado *), ele dirá que rejeita a hipótese de que as médias sejam iguais.
Mas, espere um momento. Ao concluir que as médias não são iguais, logicamente também se deve concluir que ambas não sejam iguais a zero! Com os mesmos dados, se forem testadas hipóteses diferentes, e se os resultados forem interpretados conforme faz a maior parte da literatura aplicada (que é uma interpretação bastante frágil), você chegará a conclusões aparentemente contraditórias!
Como o p-valor traz “mais evidência” contra a hipótese de que as médias seja iguais do que contra a hipótese de que ambas sejam iguais a zero, tendo em vista que se rejeitarmos a primeira, logicamente temos que rejeitar a segunda? O que está acontecendo?
Para entender melhor, lembremos o que é o p-valor. O p-valor calcula a probabilidade de a estatística de teste ser tão grande, ou maior, do que a estatística de teste observada. Intuitivamente, o p-valor tenta responder a seguinte pergunta: se eu adotasse esta discrepância observada como evidência suficiente para rejeitar a hipótese nula, quantas vezes este teste me levaria a erroneamente rejeitar esta hipótese quando ela é de fato verdadeira. Isto é, o p-valor leva em consideração em seu cálculo todos aqueles resultados amostrais que gerariam estatísticas tão extremas quanto a observada, que poderiam ter ocorrido mas não ocorreram.
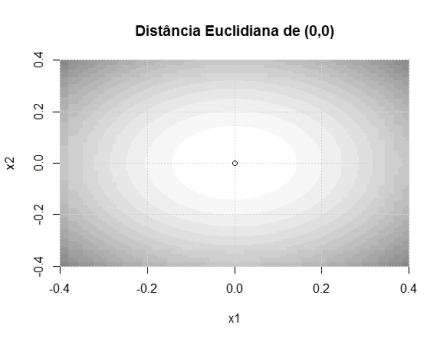
Repare como calculamos a estatística 1 e note o termo (x1^2+x2^2). Percebe-se que a estatística se torna mais extrema cada vez que o ponto (x1, x2) se distancia de (0,0) – em qualquer direção. Isto é, ela cresce com relação à distância euclidiana de (x1,x2) em relação ao ponto (0,0). Talvez isso seja mais fácil de entender com imagens. No gráfico abaixo, quanto mais escura a cor, maior é o valor da estatística de teste.
Já na estatística 2, perceba que o termo principal é (x1 – x2)^2, e o que se mede é a distância do ponto em relação à curva x1=x2. Isto é, a distância absoluta de x1 em relação a x2. Vejamos as curvas de nível. Note que ao longo da curva há diversas regiões em branco, mesmo quando distantes do ponto (0,0), pois o que a estatística mede é a distância entre os pontos x1 e x2 entre si.
Agora deve ficar mais fácil de entender o que está acontecendo. O p-valor calcula a probabilidade de encontrar uma estatística tão grande ou maior do que a observada. Ao calcular (x1 – x2)^2, todos os pontos que são distantes de (0,0), mas são próximos entre si, não geram estatísticas extremas. Como uma imagem vale mais do que mil palavras, façamos mais uma. No gráfico abaixo, os pontos pretos são todos aqueles cuja estatística de teste supera a estatística observada (0.14, -0.16). Já os pontos azuis e vermelhos são todos os pontos que tem uma estatística de teste maior do que a observada, medidos pela distância euclidiana em relação à reta x1=x2.
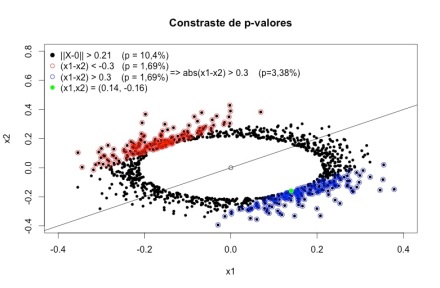 Note que vários pontos pretos que se encontram “longe” de (0,0) não são nem vermelhos nem azuis, pois estão “pertos” da reta x1=x2. Fica claro, portanto, porque o p-valor da segunda estatística é menor. Isso ocorre porque resultados extremos que discordariam bastante de (0,0) – como (0.2, 0.2) ou (0.3, 0.3) – não são considerados em seu cálculo. Note que é possível obter um p-valor ainda menor (1,6%) testanto a hipóse de que média 1 seja menor ou igual à média 2. E se a média 1 não é menor ou igual a média 2, isso implica que elas não são iguais a si, e que também não são ambas iguais a zero. É importante ter claro também que todas as estatísticas são derivadas pelo mesmo método – razão de verossimilhanças – e possuem propriedades ótimas, não são estatísticas geradas ad-hoc para provocar um resultado contra-intutivo.
Note que vários pontos pretos que se encontram “longe” de (0,0) não são nem vermelhos nem azuis, pois estão “pertos” da reta x1=x2. Fica claro, portanto, porque o p-valor da segunda estatística é menor. Isso ocorre porque resultados extremos que discordariam bastante de (0,0) – como (0.2, 0.2) ou (0.3, 0.3) – não são considerados em seu cálculo. Note que é possível obter um p-valor ainda menor (1,6%) testanto a hipóse de que média 1 seja menor ou igual à média 2. E se a média 1 não é menor ou igual a média 2, isso implica que elas não são iguais a si, e que também não são ambas iguais a zero. É importante ter claro também que todas as estatísticas são derivadas pelo mesmo método – razão de verossimilhanças – e possuem propriedades ótimas, não são estatísticas geradas ad-hoc para provocar um resultado contra-intutivo.
Para não alongar muito este post, frise-se que o que deve ser tirado como lição principal é que o p-valor não é uma medida absoluta de suporte à hipótese que está sendo testada. Mas como interpretar melhor os resultados acima? Caso você queira continuar no âmbito frequentista, algumas medidas seriam, por exemplo, não considerar literalmente as hipóteses nulas (isto é, não rejeitar ou aceitar uma hipótese precisa como x1=x2 ou x1=x2=0), avaliar que discrepâncias em relação à hipótese nula são ou não relevantes (do ponto de vista científico, e não estatístico) e conferir a função poder e intervalos de confiança para algumas alternativas de interesse. Trataremos disso mais a frente (caso vocês ainda não tenham enjoado do assunto!).

Post (e blog) bastante interessante!
Eu gosto do exemplo apresentado nesse artigo: “Aesthetics and Power Considerations in Multiple Testing – A Contradiction?” (Hommel e Bretz) http://onlinelibrary.wiley.com/doi/10.1002/bimj.200710463/abstract
Ele consiste em uma regressão linear com dois coeficientes, beta_1 e beta_2. Os autores mostram procedimentos (já corrigidos para comparações multiplas etc) que levam a hipótese beta_1=0 a ser rejeitada, mas não a hipótese beta_1=beta_2=0.
O que me incomoda nesses exemplos não é tanto o pvalor não ser “coerente” (já que como você falou, ele não é uma medida de evidência), mas o fato de termos uma contradição no resultado dos testes: por mais que em geral não se interpreta “não-rejeitar” como “aceitar”, ainda costumamos interpretar “rejeitar” como “rejeitar”. E bem, se rejeitamos beta_1=0, devemos rejeitar beta_1=beta_2=0, não?
CurtirCurtir
Obrigado pelos comentários, Rafael!
Pelo que você descreve, me parece que o “problema” é similar ao exemplo. Na maior parte dos casos penso que avaliar a função poder e que discrepâncias os dados sugerem na “rejeição” e na “não-rejeição” ajuda a resolver a contradição. De modo simplificado, se você ao invés de pensar em termos de hiptóteses precisas (pois em geral o teste não tem precisão infinita e não consegue distinguir certos valores da nula), então não haveria problema rejeitar que beta_1 esteja a partir de certa distância de zero e, ao mesmo tempo, dizer que não é possível assegurar que o vetor (beta_1, beta_2) esteja a partir de certa distância de (0,0) – isso porque tanto as medidas de discrepância quanto a sensibilidade dos testes são diferentes. Mas acho melhor baixar o artigo para ler antes de comentar e talvez seja mais fácil ver o que está ocorrendo com simulações!
Abs
CurtirCurtir
Não obrigatoriamente, Rafael. Complementando o que o Carlos comentou, nós não temos mais um intervalo de confiança quando testamos estas duas restrições lineares ao mesmo tempo. Temos uma região de confiança e isto agora também depende da estrutura de covariância entre os dois estimadores. Se houver independência (ou o caso mais fraco de não autocorrelação), essa “contradição” não existirá.
Em termos de álgebra linear, as projeções são feitas em espaços diferentes. Não haverá a “contradição” se houver ortogonalidade.
CurtirCurtir
Fernando, o que você menciona também é algo muito importante, pois, a depender da estrutura de covariância, testes marginais e testes conjuntos podem difererir substancialmente! Entretanto, este tipo de situação pode ocorrer mesmo quando as variáveis são independentes em testes conjuntos. Abs
CurtirCurtir
Ah, acho que é verdade isso. No caso bivariado, por exemplo, quando as variáveis forem independentes a região de confiança será um círculo. Quando a correlação vai mudando o formato passa a ser “mais” elíptico.
No caso que eu pensei, teríamos uma região de confiança quadrada quando as variáveis fossem independentes (sobrepondo os dois intervalos de confiança no mesmo plano).
CurtirCurtir
Pingback: P-Valor: a explicação didática definitiva | De Gustibus Non Est Disputandum
Pingback: P-valor (para as aulas de 2019) – De Gustibus Non Est Disputandum