Suponha que você queira medir o efeito de X em Y (isto é, o quanto uma variação de X afeta Y – uma relação causal) e que você tenha mais duas variáveis que podem ser incluídas como controle, Z1 e Z2. Suponha ainda que você saiba que o modelo é linear, isto é, não há nenhuma incerteza com relação à especificação. Quais variáveis você incluiria no seu modelo?
Hoje, provavelmente você diria o seguinte: depende da significância! São Z1 e Z2 significantes? Se sim, eles devem ser incluídos.
Vejamos um exemplo de uma simulação. O código em R está ao final do post.
Vamos rodar as três regressões: uma só com X, outra incluindo Z1 e por fim uma com todos os controles. Os resultados foram os seguintes:
Equação 1: Y = -10 + 43X ***
Equação 2: Y = -7 + 13X * + 107Z1 ***
Equação 3: Y = -5 – 9X * + 46Z1 *** + 37Z2 ***
Pelos resultados, tanto Z1 quanto Z2 são significantes, então preferimos a equação 3. Concluímos que, na média, uma variação de 1 unidade de X reduz Y em 9 unidades. Certo?
***
Errado. O modelo ideal neste caso seria a equação 2. O efeito real de X sobre Y é de 10 (veja que valor estimado foi 13, bem próximo). O problema aqui é que a significância estatística não vai te responder sobre a pertinência de incluir ou não uma variável para estimar o efeito de X sobre Y. Infelizmente, não há almoço grátis. Como diz Judea Pearl, sem saber a estrutura do problema, não é possível determinar quais variáveis devem ser incluídas. Agora pense. Como é a lógica de trabalho dos artigos aplicados hoje? *** A simulação A nossa simulação tem a seguinte estrutura (U1 e U2 dizem respeito a duas variáveis não observadas, só observamos Y, X, Z1 e Z2):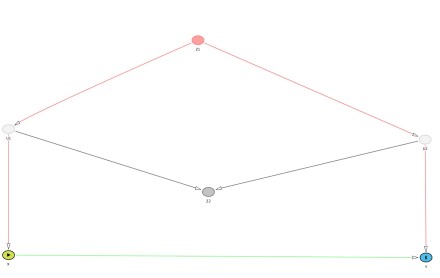 
O código em R para gerar os resultados é:
gen_data <- function(N=200,s=2,beta1=10, beta2=100){
Z1 <- rnorm(N,0,s)
U2 <- rnorm(N,0,s) + Z1
U1 <- rnorm(N,0,s) + Z1
Z2 <- rnorm(N,0,s) + U2 + U1
X <- rnorm(N,0,s) + U1
Y <- rnorm(N,0,s) + beta1*X + beta2*U2
data.frame(Y,X,Z1,Z2)
}
set.seed(100)
data <- gen_data()
summary(lm(Y~X, data))
summary(lm(Y~X + Z1, data))
summary(lm(Y~X + Z1 + Z2, data))
Você pode brincar mais com o paradoxo de Simpson aqui; e o gráfico você pode fazer aqui.
Análise Real 
Pingback: useR! 2014 | Análise Real
Pingback: Causalidade e Paradoxo de Simpson: debate acalorado entre Judea Pearl x Andrew Gelman. | Análise Real
Pingback: Retrospectiva: posts mais lidos de 2014 | Análise Real
O problema, a meu ver, é que a DAG “verdadeira” não é conhecida (e nem deve existir). Na prática, a escolha é arbitrária. Pode-se escolher pela significância, ou pode-se inventar uma DAG para justificar a seleção.
CurtirCurtir
Isso não é um problema, o exemplo apenas ilustra o fato inevitável de que, se o cientista não tiver conhecimento nenhum além da distribuição de probabilidade dos dados observados, não é possível decidir que “controles” incluir na regressão para identificar efeitos causais. Se o cientista quer analisar o efeito causal de X em Y, ele precisa colocar na mesa pressupostos causais para discussão, o DAG é uma forma de representar e derivar as implicações lógicas desses pressupostos de maneira transparente e eficiente. Se você discorda de uma teoria substantiva (não estatística), isso faz parte da ciência, e se o modelo causal está ali explícito você pode apontar onde reside a discordância e possivelmente verificar o quão sensível as conclusões são com relação ao pressuposto do qual você discorda.
Para contrastar, muitos pesquisadores ainda usam significância estatística como critério para incluir variáveis com o objetivo de fazer inferência causal, o que é logicamente errado (como mostra o exemplo). E muitos pesquisadores teriam conhecimento adequado sobre seu objeto de pesquisa, mas ainda não tem o ferramental para traduzir formalmente esse conhecimento e decidir se devem ou não incluir as variáveis na regressão (veja o paradoxo do peso do bebe em epidemiologia por exemplo, https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4190521/). Ter uma matemática para causalidade ajuda a disciplinar esse tipo de raciocínio, e verificar se de fato as conclusões que os pesquisadores estão fazendo são derivadas de seus pressupostos.
CurtirCurtir
A DAG ajuda a modelar e entender um pouco as relações entre as variáveis, mas ela não dá a relação causal verdadeira como alguns imaginam. Já vi gente inferindo com convicção que encontrou um efeito causal simplesmente por que seguiu o “protocolo”. Você tem todo o direito de não achar isso um problema. Eu continuo achando problemático. O termo “Modelos causais” induze o analista a achar que está de fato encontrando um efeito causal, se for significativo e seguir o protocolo. O que não é verdade, o efeito pode ser simplesmente uma correlação espúria por modelagem equivocada. Esperemos mais uns anos para ver o que a ciência virará. Gente encontrando efeitos causais a torto e a direito. Na economia já vi vários exemplos.
CurtirCurtir
Não existe protocolo para encontrar efeitos causais — acho que você está se baseando na literatura atual de algumas ciência sociais, como economia ou ciência política, em que o pessoal decora um punhado de métodos, tipo variáveis instrumentais, controle sintético, e aplica esses métodos em uma base de dados sem considerações sobre pressupostos. Muitos desses analistas não aprenderam causal modeling, aprenderam “estratégias de identificação” e a seguir receitas…
O termo causal modeling é ideal, para diferenciar de statistical modeling. Do contrário o que veremos são os casos como acima, em que um analista aplica 2SLS ou OLS ou Propensity Score Matching — métodos estatísticos — e acha que está fazendo causal modeling. Se alguém quer fazer inferência causal, o modelo causal tem de estar claramente articulado para ser submetido ao escrutínio de outros cientistas. Se evitarmos modelos causais, as pessoas vão fazer inferência causal da forma como faziam antigamente e ainda fazem hoje, falando que está medindo associação mas na prática concluindo causalidade, sem sequer entender quando e como podem iferir causalidade. Essa alternativa é bem pior.
CurtirCurtir
Como se verificam os pressupostos causais da DAG?
CurtirCurtir
Alguns DAGs podem ter consequências testáveis com dados observacionais, i.e., o modelo causal implica restrições na distribuição de probabilidade observável.
Quando isso acontece, você pode testar se essa restrição se verifica na sua base de dados. Por exemplo, o modelo clássico de variável instrumental, quando as variáveis são binárias, tem implicações testáveis (https://ftp.cs.ucla.edu/pub/stat_ser/R211-U.pdf).
Mas nunca dá para testar todas os pressupostos de um modelo causal (a não ser fazendo experimentos), então as conclusões sempre são contigentes aos pressupostos que você consegue defender. No limite você pode verificar o quão sensível a sua conclusão é a certas violações dos pressupostos. Um caso famoso é o de cigarro e câncer— como a associação entre os dois é muito grande, um fator latente teria que ser muito forte para explicar a associação observada, e a maioria dos cientistas julgou tal magnitude de associação implausível.
CurtirCurtir
Escolher covariáveis na regressão continua sendo arbitrário. Se o modelo for minimamente complexo, para cada DAG que você defina, eu crio outras tantas plausíveis que induzem a escolher um conjunto diferente de covariáveis com coeficientes significativos. Mas é isso. Minhas próximas intervenções serão por meio de artigos científicos. Abraços
CurtirCurtir
Escolher covariáveis para incluir na regressão, com o intuito de identificação de um efeito causal, não é algo arbitrário! É um problema bem definido e inclusive com soluções completas para modelos causais não paramétricos. A solução depende de um input importante: conhecimento científico. E dependendo do conhecimento e do que você consegue medir, a solução pode ser “não há informação suficiente para identificar o efeito” por exemplo.
Isso é o correto! O máximo que você consegue com a distribuição observável é definir uma classe de modelos equivalentes (e até para isso precisamos de pressupostos, mais fracos, certamente, substantivos). Se o cientista não tem argumentos científicos para distinguir modelos observacionalmente equivalentes, ele não consegue fazer inferência para além daquela classe de modelos, e aqui entraria uma análise de sensibilidade. Desafiar um cientista com modelos alternativos que explicam os dados é natural, e faz parte da modelagem causal! O ponto é que a discussão do modelo causal não é de estatística, mas de ciência, essa separação é importante.
CurtirCurtir
Fundamentos de estatística trata até do problema de tradução de uma hipótese científica para a hipótese matemática, princípios inferenciais, desideratas que geram axiomas da probabilidade, lógicas paraconsistentes, entre outros assuntos, não vejo porque não seria assunto também o estudo de efeito causal entre variáveis definidas dentro de um modelo estatístico. Temos muita filosofia na estatística, não vejo pq a causalidade não possa ser um tópico de pesquisa dos fundamentos da estatística. Judea Pearl disse que não é parte da estatística, mas para mim é parte dos fundamentos da estatística.
Do jeito que é posto pelo Judea Pearl, esses modelos não modelam efeitos causais como eu os compreendo. Eles modelam um tipo de “efeito causal” definido dentro de um domínio bem específico de aplicação. Causalidade é um assunto filosófico bem profundo, modelos matemáticos não tocam nem a superfície da questão. É preciso recortar a realidade e simplificar bem as relações para usar uma DAG. A realidade é bem mais complexa do que uma ou um conjunto de DAGs.
CurtirCurtir
A estatística como uma área ampla das ciências pode e deve abraçar o estudo de modelos causais.
Mas o primeiro passo é reconhecer que a teoria estatística tradicional não tem ferramentas para isso. Por exemplo, um teste simples que ilustra isso: como *definir* o seguinte objeto — o valor esperado de Y dada uma intervenção que force todos os indivíduos da população a terem X=x?
CurtirCurtir
Não parece ser nada difícil. Basta definir um modelo de probabilidade para os elementos da população que tenham a característica X=x. No fundo nem precisa carregar na notação, mas se quiser ai vai
(O_x, A_x, P_x)
em que O_x são os valores experimentais Y que ocorrem para indivíduos que tem a característica X=x. A_x a sigma algebra e P_x a medida de probabildade de Y considerando apenas elementos que tenham a característica X=x.
Esperança de Y:
E_x(Y) = int y P_x(y)
Em modelos de regressão vc pode inclusive relaxar isso para o caso em que X \in {x1, …}
Qual a dificuldade?
CurtirCurtir
Note que o modelo (O_x, A_x, P_x) pode ser obtido também condicionalizando um modelo “maior”. Basta estabelecer condições de regularidade para que isso seja possível.
Modelagem estatística e probabilística é uma área muito rica.
CurtirCurtir
Não é questão de dificuldade (ainda!), mas só esse exercício já levanta várias nuances importantes.
A maioria das pessoas começaria definido erroneamente essa quantidade como E[Y|X=x], e não teria a o cuidado de separar o Y e X observados do Y_x e X = x experimental (no seu caso o O_x com P_x).
A sua definição está quase ok, só faltaria trocar “para os elementos da população que tenham a característica X=x” para “supondo que todos os elementos da população sejam forçados a ter X = x”, pois nós queremos o valor esperado na população inteira, não somente naqueles que observamos ter X=x.
Por enquanto temos uma nova variável intervencional (não observada) O_x com uma nova distribuição (não observada) intervencional P_x. Agora imagine o seguinte. Suponha que eu queira representar o pressuposto de que intervenções em X não afetam o valor Z. Ou que, se eu intervir manualmente fixar W = w, intervenções em X não alteram mais o valor de Y? Depois, precisamos definir uma regra de inferência de como conectar os não observáveis P_x e O_x para os observáveis P e O (do contrário não conseguimos fazer inferência, pois só temos os dados observáveis).
As soluções para essas perguntas vão acabar coincidindo com o arcabouço de respostas potencias (potential outcomes), que começou com Neyman e se popularizou com Rubin (https://www.jstor.org/stable/27590541?seq=1#metadata_info_tab_contents). Ou com o arcabouço de equações estruturais do Pearl, Heckman etc. É possível demonstrar que esses dois arcabouços são logicamente equivalentes.
Aí que começamos a entrar em questões técnicas. Por exemplo, representar pressupostos causais com variáveis potenciais tem complexidade super-exponencial e não existem algoritmos eficientes para derivar suas implicações lógicas. Já se você você representar esses pressupostos com um DAG, nós temos algoritmos completos para várias classes de problemas.
CurtirCurtir
Bom, basta mudar para O_x contém os valores experimentais Y que ocorrem para indivíduos que foram forçados a ter/receber/whatever X=x. Dá na mesma, o modelo será o mesmo só muda o palavrório.
“Suponha que eu queira representar o pressuposto de que intervenções em X não afetam o valor Z. Ou que, se eu intervir manualmente fixar W = w, intervenções em X não alteram mais o valor de Y?”
“Intervenções em X não afetam o valor de Z”: Basta definir o espaço de probabilidade de Z por (O, A, P) para qualquer valor X=x. Ou seja, o modelo de probabilidade (ou estatístico) de Z não depende de valores observados de X.
“Se fixar W = w, intervenções em X não alteram mais o valor de Y”: Poderíamos considerar
(O_w, A_w, P_w) como sendo o modelo de probabilidade (ou estatístico) de Y para todo X.
Podemos resolver isso com equações de funções, com DAGs. Não importa. A questão fundamental é que disso tudo nada tem a ver com causalidade. É apenas modelagem matemática/probabilística de dependência funcional entre variáveis, associação entre variáveis, etc…. mas não é um estudo de causalidade. É uma maneira de formalizar uma modelagem que seja mais transparente. Mas não aceito o nome modelo causal. Esse termo tem implicações fortes.
Mas tudo bem… Vamos ver o que vai acontecer com a ciência nos próximos anos. Daqui a 30 anos conversamos sobre isso de novo.
valeu pela discussão
CurtirCurtir
Bom mas imagina o cientista que quer definir se o ato de fumar cigarro aumenta a chance de câncer de pulmão (não apenas se fumar cigarro está associado com câncer de pulmão). Esse cientista tem que colocar pressupostos na mesa que vão além da P(X) (a distribuição de probabilidade observada das variáveis). Como chamar esse tipo de modelagem, se não modelagem causal?
CurtirCurtir
É uma modelagem estatística. Pra mim, não tem nada de causal aí. A modelagem estatística pode ser justificada por meio de argumentos físicos, matemáticos, biológicos ou simplesmente por ignorância. Só pq se apresenta um gráfico mostrando uma possível relação entre as variáveis de interesse, não significa que seja uma modelagem causal. Claramente as DAGs não podem ser verificadas, podem em alguns casos ser descartadas, mas nunca aceitas como verdadeiras como qualquer hipótese científica/estatística.
CurtirCurtir
Acho que para resolver esse impasse o ideal é definir formalmente o que é um modelo estatístico e o que é um modelo causal.
Minha definição de modelo estatístico é uma coleção de pressupostos sobre a distribuição de probabilidade das variáveis observáveis P(V). Um modelo estatístico não descreve como o sistema se comporta sob intervenções. A restrição para variáveis observáveis é para não se esconder pressupostos causais em variáveis latentes como O_x (a variável O sob o regime de intervenção X).
Já um modelo causal é uma coleção de pressupostos sobre como o sistema se comporta sob diferentes intervenções—-o que pode ou não impor restrições em P(V).
CurtirCurtir
O modelo estatístico pra mim é como eu defino em: https://www.ime.usp.br/~patriota/Statistical-Model.gif ou na minha apresentação: https://www.ime.usp.br/~patriota/On-Assumptions-NHST.pdf
O vetor aleatório Z = (X,gamma), em que X é um vetor aleatório de observáveis e gamma um vetor aleatório de não-observáveis (variáveis latentes) está bem definido no modelo estatístico. Há uma estrutura funcional entre as variáveis do vetor Z. Temos como casos particulares modelos de equações estruturais, modelos mistos, modelos heteroscedásticos, modelos não lineares, séreis temporias, etc. A modelagem pode ser justificada por meio de DAGs, sem problemas. Apesar de que DAGs acabam restringindo muito a aplicação, pois, em modelos estatísticos, estruturas mais complexas poderiam ser modeladas.
O “Modelo causal” pode até ter algo a mais do que apenas estrutura funcional entre as variáveis do vetor Z, mas não acho que esse termo ajuda. Não se está modelando causa de fato, pode ser apenas uma relação espúria. “Ahh no meu modelo causal eu coloquei uma relação espúria entre W e Y.” Quem é que define se a relação é espúria ou não? É o mesmo problema da correlação, só por que foi definida na DAG uma relação causal entre W e Y não significa que tenha alguma relação causal de fato.
O P(Y=y| do(X=x)) dele eu escreveria como P_x(Y=y). A primeira confunde com prob condicional, já no segundo fica claro que a distribuição de probabilidade é para os indivíduos que tiverem os valores de X fixados em x. A parte contrafactual que o Judea Pearl discute é interessante. Eu ainda quero ver se há outras maneiras de definir o Y_x(u) dele.
CurtirCurtir
Veja que na sua definição de modelo estatístico não há uma semântica para ações—não há uma representação formal do que muda e do que não muda em P quando se intervém em um conjunto de variáveis. Você pode tentar remediar isso criando variáveis intervencionais O_x. Mas note que você vai ter que fazer isso para cada intervenção concebível, o que é algo intratável.
Na verdade para surgir esse problema, nem precisamos de probabilidade. Imagine um modelo determinístico de causa e efeito com P variáveis, e imagine que você vai tentar representar o modelo somente usando proposições lógicas clássicas. Seu modelo vai ser uma lista não somente todas as possíveis ações concebíveis, mas todas consultas concebíveis que poderíamos fazer ao modelo. Ou seja, é impossível a não ser para P bem pequeno.
Nós usamos as duas notações, muitos dos papers usam P_x(Y=y) (aqui por exemplo https://ftp.cs.ucla.edu/pub/stat_ser/R290-L.pdf)
O uso de P(Y=y| do(X=x)) é mais para facilitar a aplicação de regras sintáticas do do-calculus, como trocar ação por observação (se permitido pelos pressupostos do modelo) P(Y=y| do(X=x))= P(Y=y| X=x). Mas esse detalhe de notação não tem implicações práticas nas derivações ou complexidade computacional.
O que tem implicações computacionais é como representar pressupostos causais e como derivar suas implicações lógicas. Por exemplo, suponha que um cientista te dê as seguintes informações:
– Minha teoria prevê que X causa Z e que Z causa Y
– Ela também prevê que, uma vez que fixamos o valor de Z via intervenção, manipulações em X não causam alterações em Y
– Existe causas comuns entre X e Y que não medi, mas não existem causas comuns entre X e Z nem entre Z e Y.
Aí ele pergunta:
(1) com base nesses pressupostos, é possível estimar usando dados observacionais qual seria a distribuição de Y dada uma intervenção uniforme na população que fixe X =x para todos indivíduos?
(2) meus pressupostos implicam em alguma implicação testável com dados observacionais?
Nossa tarefa é traduzir formalmente esses pressupostos, e verificar de maneira eficiente e automática: (i) se eles são suficientes para responder (1) e se sim, qual o funcional de P que dá a resposta correta, (ii) além de verificar (2) e dizer para o pesquisador se há e quais as implicações testáveis de sua teoria.
Acho que um exercício interessante seria tentar formalizar esse problema antes de ler a literatura! Depois tentar pensar numa solução para o problema assim considerando um modelo arbitrário, isso dá um flavor do problema que está se tentando resolver.
CurtirCurtir
Eu ainda vou analisar com cuidado os fundamentos do modelo probabilístico causal. Ele define o “modelo causal” pela tripla:
M = ,
sendo
U = conj de v.a.’s exógenas,
V = conj de v.a.ś endógenas,
F = conjunto de funções mapeando as relações de v.a.’s exógenas e endógenas.
Ele também define o submodelo
Mx = ,
em que Fx é formado deletando todas as funções que se conectam a X substituindo-as por funções constantes e iguais a x.
O modelo “causal” probabilístico é definido por
,
em que P é uma medida de probabilidade definida sobre a variável U da qual todas as variáveis exógenas são funções. Ou seja, quaisquer variáveis endógenas X e Y podem ser escrita como funções de U: X = f_X(U) e Y = f_Y(U).
Todas as medidas de probabilidade são funções de P(U=u). Não há um modelo de probabilidade especial para o caso em que se força a ter X=x, bastaria usar o submodelo Mx.
A estrutura relacional M definiria as relações entre as variáveis em Z = (X,gamma) no meu modelo estatístico, em que X faria o papel de V e gamma faria o papel de U e F descreveria as relações entre eles (ou seja, define a estrutura do modelo estatístico).
A estrutura relacional Mx é usada para obter Y_x(U). Para mim, esse sim é um conceito novo e eu ainda estou pensando o que de fato decorre dele em termos de variáveis aleatórias no contexto do modelo estatístico.
Basicamente a probabilidade de Y_x(U) ser igual a y é definida por:
(***) P(Y_x(U) = y) = sum_{u in Ax(y) } P(U = u)
em que Ax(y) = {u: Y=y sob a estrutura Mx}.
Na notação dele, a medida de probabilidade P continua a mesma. Ele muda a estrutura relacional de M para Mx. Essa probabilidade (***) é uma definição nova e eu ainda estou estudando suas implicações.
CurtirCurtir
Eu ainda vou analisar com cuidado os fundamentos do modelo probabilístico causal. Ele define o “modelo causal” pela tripla:
M = (U,V,F),
sendo
U = conj de v.a.’s exógenas,
V = conj de v.a.ś endógenas,
F = conjunto de funções mapeando as relações de v.a.’s exógenas e endógenas.
Ele também define o submodelo
Mx = (U,V,Fx),
em que Fx é formado deletando todas as funções que se conectam a X substituindo-as por funções constantes e iguais a x.
O modelo “causal” probabilístico é definido por
(M,P),
em que P é uma medida de probabilidade definida sobre a variável U da qual todas as variáveis exógenas são funções. Ou seja, quaisquer variáveis endógenas X e Y podem ser escrita como funções de U: X = f_X(U) e Y = f_Y(U).
Todas as medidas de probabilidade são funções de P(U=u). Não há um modelo de probabilidade especial para o caso em que se força a ter X=x, bastaria usar o submodelo Mx.
A estrutura relacional M definiria as relações entre as variáveis em Z = (X,gamma) no meu modelo estatístico, em que X faria o papel de V e gamma faria o papel de U e F descreveria as relações entre eles (ou seja, define a estrutura do modelo estatístico).
A estrutura relacional Mx é usada para obter Y_x(U). Para mim, esse sim é um conceito novo e eu ainda estou pensando o que de fato decorre dele em termos de variáveis aleatórias no contexto do modelo estatístico.
Basicamente a probabilidade de Y_x(U) ser igual a y é definida por:
(***) P(Y_x(U) = y) = sum_{u in Ax(y) } P(U = u)
em que Ax(y) = {u: Y=y sob a estrutura Mx}.
Na notação dele, a medida de probabilidade P continua a mesma. Ele muda a estrutura relacional de M para Mx. Essa probabilidade (***) é uma definição nova e eu ainda estou estudando suas implicações.
CurtirCurtir
Mas apenas reforço, não vejo motivos para chamar esse modelo de “modelo causal”. Para mim é uma estrutura relacional entre variáveis.
CurtirCurtir