Autor: Carlos Cinelli
Culto da significância estatística – alterando a base de dados.
O foco em encontrar resultados ‘significantes’ gera coisas bizarras:
“Fox came to me to apologize after he admitted to the fabrication. He described how and why he started tampering with data. The first time it happened he had analyzed a dataset and the results were just shy of significance. Fox noticed that if he duplicated a couple of cases and deleted a couple of cases, he could shift the p-value to below .05. And so he did. Fox recognized that the system rewarded him, and his collaborators, not for interesting research questions, or sound methodology, but for significant results. When he showed his collaborators the findings they were happy with them—and happy with Fox.”
Kenneth Arrow faleceu
Um daqueles economistas que sequer precisa de introdução. Deixo aqui matéria do NYT. Certamente aparecerão várias outras.
Regressão robusta, erro de medida e preços de imóveis
Um amigo estava tendo problemas ao analisar sua base de dados e pediu ajuda — ao olhar alguns gráficos o problema parecia claro: erro de medida. Resolvi revisitar um post antigo e falar um pouco mais sobre como poucas observações influentes podem afetar sua análise e como métodos robustos podem te dar uma dica se isso está acontecendo.
Voltemos, então, ao nosso exemplo de uma base de dados de venda de imóveis online:
arquivo <- url("https://dl.dropboxusercontent.com/u/44201187/dados/vendas.rds")
con <- gzcon(arquivo)
vendas <- readRDS(con)
close(con)
Suponha que você esteja interessado na relação entre preço e tamanho do imóvel. Basta um gráfico para perceber que a base contém alguns dados muito corrompidos:
with(vendas, plot(preco ~ m2))

Mas, não são muitos pontos. Nossa base tem mais de 25 mil observações, será que apenas essas poucas observações corrompidas podem alterar tanto assim nossa análise? Sim. Se você rodar uma regressão simples, ficará desapontado:
summary(m1 <- lm(preco ~ m2, data = vendas))
## ## Call: ## lm(formula = preco ~ m2, data = vendas) ## ## Residuals: ## Min 1Q Median 3Q Max ## -6746423 -937172 -527498 99957 993612610 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 1386226.833 18826.675 73.631 < 0.0000000000000002 *** ## m2 18.172 3.189 5.699 0.0000000121 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 9489000 on 254761 degrees of freedom ## Multiple R-squared: 0.0001275, Adjusted R-squared: 0.0001235 ## F-statistic: 32.48 on 1 and 254761 DF, p-value: 0.00000001208
A regressão está sugerindo que cada metro quadrado extra no imóvel corresponde, em média, a um aumento de apenas 18 reais em seu preço! Como vimos no caso do post anterior, limpar um percentual bem pequeno da base é suficiente para estimar algo que faça sentido.
Mas, suponha que você não tenha noção de quais sejam os outliers da base e também que, por alguma razão, você não saiba que 18 reais o metro quadrado é um número completamente absurdo a priori. O que fazer? (Vale fazer um parêntese aqui – se você está analisando um problema em que você não tem o mínimo de conhecimento substantivo, não sabe julgar sequer se 18 é um número grande ou pequeno, plausível ou não, isso por si só é um sinal de alerta, mas prossigamos de qualquer forma!)
Um hábito que vale a pena você incluir no seu dia-a-dia é rodar regressões resistentes/robustas, que buscam levar em conta a possibilidade de uma grande parcela dos dados estar corrompida.
Vejamos o que ocorre no nosso exemplo de dados online:
library(robust) summary(m2 <- lmRob(preco ~ m2, data = vendas))
## ## Call: ## lmRob(formula = preco ~ m2, data = vendas) ## ## Residuals: ## Min 1Q Median 3Q Max ## -3683781389 -202332 -23119 64600 994411077 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -15926.247 589.410 -27.02 <0.0000000000000002 *** ## m2 9450.762 5.611 1684.32 <0.0000000000000002 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 171800 on 254761 degrees of freedom ## Multiple R-Squared: 0.4806 ## ## Test for Bias: ## statistic p-value ## M-estimate 502.61 0 ## LS-estimate 86.91 0
Agora cada metro quadrado correponde a um aumento de R$9.450,00 no preço do imóvel! A mensagem aqui extrapola dados online, que são notórios por terem observações com erros de várias ordens de magnitude. Praticamente toda base de dados que você usa está sujeita a isso, mesmo de fontes oficiais. No post anterior vimos um exemplo em que pesquisadores não desconfiaram de uma queda de 36% (!!!) do PIB na Tanzânia.
Por fim, vale fazer a ressalva de sempre: entender o que está acontencedo nos seus dados — por que os valores são diferentes e a razão de existir de alguns outliers — é fundamental. Dependendo do tipo de problema, os outliers podem não ser erros de medida, e você não quer simplesmente ignorar sua influência. Na verdade, há casos em que outliers podem ser a parte mais interessante da história.
Vídeos da RStudio Conference disponíveis
Os vídeos da conferência do RStudio já estão disponíveis aqui.
Daniel Kahneman e a replicação dos estudos de priming
A crise de replicabilidade obriga Kahneman a rever sua posição. Algo louvável diante de tantos pesquisadores que insistem em continuar no erro:
PS: isso é um comentário do Daniel Kahneman neese post aqui.
Google Trends no R
O pacote gtrendsR está passando por uma reformulação e parece que vai ficar ainda mais fácil analisar dados do Google Trends no R. A nova versão ainda não está no CRAN, mas já pode ser testada pelo github. Para instalar:
install.packages("devtools")
devtools::install_github('PMassicotte/gtrendsR', ref = 'new-api')
A grande novidade dessa versão é que não será mais preciso fazer login no google trends para ter acesso. Para brasileiros, outra novidade é que os bugs com problema de encoding parecem estar diminuindo.
Vejamos um exemplo simples, pegando dados das buscas pelos nomes dos candidatos nas eleições de 2014 no Brasil:
library(gtrendsR)
eleicoes2014 <- gtrends(c("Dilma Rousseff", "Aécio Neves", "Marina Silva"), geo = c("BR"), time = "2014-01-01 2014-12-31")
plot(eleicoes2014)
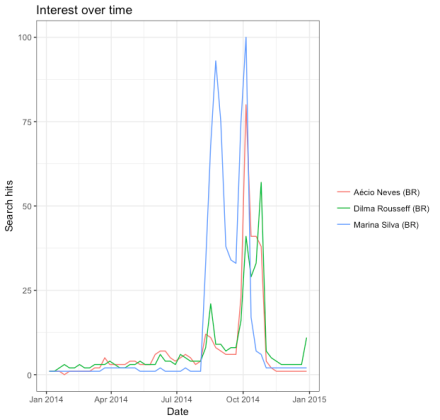
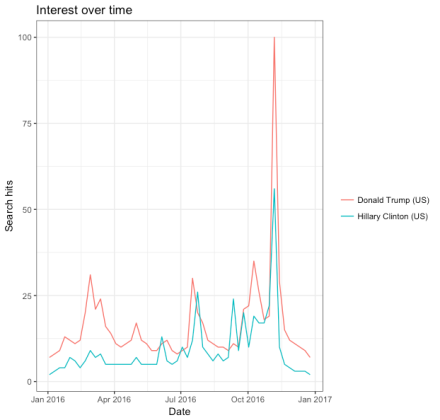
Para ilustrar novamente, vejamos um exemplo mais recente — as buscas pelos nomes dos candidatos das eleições norte-americanas:
USelections2016 <- gtrends(c("Donald Trump", "Hillary Clinton"), geo = c("US"), time = "2016-01-01 2016-12-31")
plot(USelections2016)
Erro de medida e ‘atenuação’ dos efeitos estimados
Andrew Gelman publicou um pequeno comentário na Science sobre erro de medida e “atenuação dos efeitos estimados”. O argumento é o seguinte: no modelo clássico de erro de medida, na média suas estimativas são puxadas para baixo. Suponha, então, que você tenha feito um experimento com amostra pequena, com erro de medida, mas ainda assim você tenha encontrado um efeito estimado “significante”. Ora, é tentador argumentar o seguinte: tanto a amostra pequena quanto o erro de medida estão “jogando contra” meu efeito estimado, então é provável que o efeito real seja ainda maior do que o que eu estimei. Parece lógico, não?
Parece, mas não é. E, infelizmente, esse raciocínio ainda engana muitos pesquisadores. Na verdade, em um contexto de efeitos reais pequenos junto com amostras pequenas, é mais provável que aquelas estimativas estatisticamente significantes estejam superestimando o efeito real. O problema aqui é que o ruído das amostras pequenas em conjunto com o viés de seleção de estimativas estatisticamente significantes predomina. Vejamos isso na prática com uma simples simulação.
No código abaixo eu simulo mil estudos com um tamanho amostral fixo (n = 10, n = 20, n = 50, n = 500 e n = 1000). Desses mil estudos, eu seleciono apenas aqueles que são estatisticamente “significantes” e coloco no gráfico o valor estimado do estudo. O valor real do efeito é 0.1, que está representado pela linha vermelha. Vejam que, para amostras até de tamanho 100, todas as estimativas “significantes” da simulação estão superestimando o efeito real. Apenas quando a amostra é grande o suficiente que o efeito atenuante do erro de medida se faz prevalecer, revertendo o resultado.

E se você comparar as estimativas com e sem erro de medida, como faz Gelman, também vai verificar que com amostras pequenas dificilmente uma é sempre maior do que a outra.
Código para simulação:
rm(list = ls())
set.seed(10)
ns = c(10, 20, 50, 100, 500, 1000)
oldpar <- par(mfrow = c(2,3))
for (n in ns) {
b = 0.1
x <- rnorm(n)
y <- b*x
coefs <- replicate(1000, {
xs <- x + rnorm(n)
ys <- y + rnorm(n)
coef(summary(lm(ys ~ xs)))[2,]
})
coefs <- t(coefs)
plot(coefs[coefs[,3] > 2, 1], ylim = c(min(c(b, coefs[,1])), max(coefs[,1])),
xlab = "Significant Experiments", ylab = "'Significant' Estimates",
main = paste("Sample size =", n), pch = 20)
abline(h = b, col = "red", lty = 2)
}
par(oldpar)
Data Frames
***
Parte do livro Introdução à análise de dados com R. Este trabalho está em andamento, o texto é bastante preliminar e sofrerá muitas alterações.
Quer fazer sugestões? Deixe um comentário abaixo ou, se você sabe utilizar o github, acesse aqui.
Não copie ou reproduza este material sem autorização.
Volte para ver atualizações!
***
Data Frames: seu banco de dados no R
Por que um data.frame?
Até agora temos utilizado apenas dados de uma mesma classe, armazenados ou em um vetor ou em uma matriz. Mas uma base de dados, em geral, é feita de dados de diversas classes diferentes: no exemplo anterior, por exemplo, podemos querer ter uma coluna com os nomes dos funcionários, outra com o sexo dos funcionários, outra com valores… note que essas colunas são de classes diferentes, como textos e números. Como guardar essas informações?
A solução para isso é o data.frame. O data.frame é talvez o formato de dados mais importante do R. No data.frame cada coluna representa uma variável e cada linha uma observação. Essa é a estrutura ideal para quando você tem várias variáveis de classes diferentes em um banco de dados.
Criando um data.frame: data.frame() e as.data.frame()
É possível criar um data.frame diretamente com a função data.frame():
funcionarios <- data.frame(nome = c("João", "Maria", "José"),
sexo = c("M", "F", "M"),
salario = c(1000, 1200, 1300),
stringsAsFactors = FALSE)
funcionarios
## nome sexo salario
## 1 João M 1000
## 2 Maria F 1200
## 3 José M 1300
Também é coverter outros objetos em um data.frame com a função as.data.frame().
Discutiremos a opção stringsAsFactors = FALSE mais a frente.
Vejamos a estrutura do data.frame. Note que cada coluna tem sua própria classe.
str(funcionarios) ## 'data.frame': 3 obs. of 3 variables: ## $ nome : chr "João" "Maria" "José" ## $ sexo : chr "M" "F" "M" ## $ salario: num 1000 1200 1300
Nomes de linhas e colunas
O data.frame sempre terá rownames e colnames.
rownames(funcionarios) ## [1] "1" "2" "3" colnames(funcionarios) ## [1] "nome" "sexo" "salario"
Detalhe: a função names() no data.fram trata de suas colunas, pois os elementos fundamentais do data.frame são seus vetores coluna.
names(funcionarios) ## [1] "nome" "sexo" "salario"
Não parece tão diferente de uma matriz…
O que ocorreria com o data.frame funcionarios se o transformássemos em uma matriz? Vejamos:
as.matrix(funcionarios) ## nome sexo salario ## [1,] "João" "M" "1000" ## [2,] "Maria" "F" "1200" ## [3,] "José" "M" "1300"
Perceba que todas as variáveis viraram character! Uma matriz aceita apenas elementos da mesma classe, e é exatamente por isso precisamos de um data.frame neste caso.
Manipulando data.frames como matrizes
Ok, temos mais um objeto do R, o data.frame … vou ter que reaprender tudo novamente? Não! Você pode manipular data.frames como se fossem matrizes!
Praticamente tudo o que vimos para selecionar e modificar elementos em matrizes funciona no data.frame. Podemos selecionar linhas e colunas do nosso data.frame como se fosse uma matriz:
## tudo menos linha 1
funcionarios[-1, ]
## nome sexo salario
## 2 Maria F 1200
## 3 José M 1300
## seleciona primeira linha e primeira coluna (vetor)
funcionarios[1, 1]
## [1] "João"
## seleciona primeira linha e primeira coluna (data.frame)
funcionarios[1, 1, drop = FALSE]
## nome
## 1 João
## seleciona linha 3, colunas "nome" e "salario"
funcionarios[3 , c("nome", "salario")]
## nome salario
## 3 José 1300
E também alterar seus valores tal como uma matriz.
## aumento de salario para o João funcionarios[1, "salario"] <- 1100 funcionarios ## nome sexo salario ## 1 João M 1100 ## 2 Maria F 1200 ## 3 José M 1300
Extra do data.frame: selecionando e modificando com $ e [[ ]]
Outras formas alternativas de selecionar colunas em um data.frame são o $ e o [[ ]]:
## Seleciona coluna nome funcionarios$nome ## [1] "João" "Maria" "José" funcionarios[["nome"]] ## [1] "João" "Maria" "José" ## Seleciona coluna salario funcionarios$salario ## [1] 1100 1200 1300 funcionarios[["salario"]] ## [1] 1100 1200 1300
Tanto o $ quanto o [[ ]] sempre retornam um vetor como resultado.
Também é possível alterar a coluna combinando $ ou [[ ]] com <-:
## outro aumento para o João funcionarios$salario[1] <- 1150 ## equivalente funcionarios[["salario"]][1] <- 1150 funcionarios ## nome sexo salario ## 1 João M 1150 ## 2 Maria F 1200 ## 3 José M 1300
Extra do data.frame: retornando sempre um data.frame com [ ]
Se você quiser garantir que o resultado da seleção será sempre um data.frame use drop = FALSE ou selecione sem a vírgula:
## Retorna data.frame funcionarios[ ,"salario", drop = FALSE] ## salario ## 1 1150 ## 2 1200 ## 3 1300 ## Retorna data.frame funcionarios["salario"] ## salario ## 1 1150 ## 2 1200 ## 3 1300
Tabela resumo: selecionando uma coluna em um data.frame
Resumindo as formas de seleção de uma coluna de um data.frame.

Criando colunas novas
Há diversas formas de criar uma coluna nova em um data.frame. O principal segredo é o seguinte: faça de conta que a coluna já exista, selecione ela com $, [,] ou [[]] e atribua o valor que deseja.
Para ilustrar, vamos adicionar ao nosso data.frame funcionarios mais três colunas.
Com $:
funcionarios$escolaridade <- c("Ensino Médio", "Graduação", "Mestrado")
Com [ , ]:
funcionarios[, "experiencia"] <- c(10, 12, 15)
Com [[ ]]:
funcionarios[["avaliacao_anual"]] <- c(7, 9, 10)
Uma última forma de adicionar coluna a um data.frame é, tal como uma matriz, utilizar a função cbind() (column bind).
funcionarios <- cbind(funcionarios,
prim_emprego = c("sim", "nao", "nao"),
stringsAsFactors = FALSE)
Vejamos como ficou nosso data.frame com as novas colunas:
funcionarios ## nome sexo salario escolaridade experiencia avaliacao_anual prim_emprego ## 1 João M 1150 Ensino Médio 10 7 sim ## 2 Maria F 1200 Graduação 12 9 nao ## 3 José M 1300 Mestrado 15 10 nao
E agora, temos colunas demais, como remover algumas delas?
Removendo colunas
A forma mais fácil de remover coluna de um data.fram é atribuir o valor NULL a ela:
## deleta coluna prim_emprego funcionarios$prim_emprego <- NULL
Mas a forma mais segura e universal de remover qualquer elemento de um objeto do R é selecionar tudo exceto aquilo que você não deseja. Isto é, selecione todas colunas menos as que você não quer e atribua o resultado de volta ao seu data.frame:
## deleta colunas 4 e 6 funcionarios <- funcionarios[, c(-4, -6)]
Adicionando linhas
Uma forma simples de adicionar linhas é atribuir a nova linha com <-. Mas cuidado! O que irá acontecer com o data.frame com o código abaixo?
## CUIDADO!
funcionarios[4, ] <- c("Ana", "F", 2000, 15)
Note que nosso data.frame inteiro se transformou em texto! Você sabe explicar por que isso aconteceu? relembrar coerção
str(funcionarios) ## 'data.frame': 4 obs. of 4 variables: ## $ nome : chr "João" "Maria" "José" "Ana" ## $ sexo : chr "M" "F" "M" "F" ## $ salario : chr "1150" "1200" "1300" "2000" ## $ experiencia: chr "10" "12" "15" "15"
Antes de prosseguir, transformemos as colunas salario e experiencia em números novamente:
funcionarios$salario <- as.numeric(funcionarios$salario) funcionarios$experiencia <- as.numeric(funcionarios$experiencia)
Se os elementos forem de classe diferente, use a função data.frame para evitar coerção:
funcionarios[4, ] <- data.frame(nome = "Ana", sexo = "F",
salario = 2000, experiencia = 15,
stringsAsFactors = FALSE)
Também é possível adicionar linhas com rbind():
rbind(funcionarios,
data.frame(nome = "Ana", sexo = "F",
salario = 2000, experiencia = 15,
stringsAsFactors = FALSE))
Atenção! Não fique aumentando um data.frame de tamanho adicionando linhas ou colunas. Sempre que possível pré-aloque espaço!
Removendo linhas
Para remover linhas, basta selecionar apenas aquelas linhas que você deseja manter:
## remove linha 4 do data.frame funcionarios <- funcionarios[-4, ]
## remove linhas em que salario <= 1150 funcionarios <- funcionarios[funcionarios$salario > 1150, ]
Filtrando linhas com vetores logicos
Relembrando: se passarmos um vetor lógico na dimensão das linhas, selecionamos apenas aquelas que são TRUE. Assim, por exemplo, se quisermos selecionar aquelas linhas em que a coluna salario é maior do que um determinado valor, basta colocar esta condição como filtro das linhas:
## Apenas linhas com salario > 1000 funcionarios[funcionarios$salario > 1000, ] ## nome sexo salario experiencia ## 2 Maria F 1200 12 ## 3 José M 1300 15 ## Apenas linhas com sexo == "F" funcionarios[funcionarios$sexo == "F", ] ## nome sexo salario experiencia ## 2 Maria F 1200 12
Funções de conveniência: subset()
Uma função de conveniência para selecionar linhas e colunas de um data.frame é a função subset(), que tem a seguinte estrutura:
subset(nome_do_data_frame,
subset = expressao_logica_para_filtrar_linhas,
select = nomes_das_colunas,
drop = simplicar_para_vetor?)
Vejamos alguns exemplos:
## funcionarios[funcionarios$sexo == "F",]
subset(funcionarios, sexo == "F")
## nome sexo salario experiencia
## 2 Maria F 1200 12
## funcionarios[funcionarios$sexo == "M", c("nome", "salario")]
subset(funcionarios, sexo == "M", select = c("nome", "salario"))
## nome salario
## 3 José 1300
Funções de conveniência: with
A função with() permite que façamos operações com as colunas do data.frame sem ter que ficar repetindo o nome do data.frame seguido de $ , [ , ] ou [[]] o tempo inteiro.
Para ilustrar:
## Com o with with(funcionarios, (salario^3 - salario^2)/log(salario)) ## [1] 2.4e+08 3.1e+08 ## Sem o with (funcionarios$salario^3 - funcionarios$salario^2)/log(funcionarios$salario) ## [1] 2.4e+08 3.1e+08
Quatro formas de fazer a mesma coisa (pense em outras formas possíveis):
subset(funcionarios, sexo == "M", select = "salario", drop = TRUE) ## [1] 1300 with(funcionarios, salario[sexo == "M"]) ## [1] 1300 funcionarios$salario[funcionarios$sexo == "M"] ## [1] 1300 funcionarios[funcionarios$sexo == "M", "salario"] ## [1] 1300
Aplicando funções no data.frame: sapply e lapply, funções nas colunas (elementos)
Outras duas funções bastante utilizadas no R são as funções sapply() e lapply().
- As funções
sapplyelapplyaplicam uma função em cada elemento de um objeto. - Como vimos, os elementos de um
data.framesão suas colunas. Deste modo, as funçõessapplyelapplyaplicam uma função nas colunas de um data.frame. - A diferença entre uma e outra é que a primeira tenta simplificar o resultado enquanto que a segunda sempre retorna uma lista.
Testando no nosso data.frame:
sapply(funcionarios[3:4], mean) ## salario experiencia ## 1250 14 lapply(funcionarios[3:4], mean) ## $salario ## [1] 1250 ## ## $experiencia ## [1] 14
Filtrando variáveis antes de aplicar funções: filter()
Como data.frames podem ter variáveis de classe diferentes, muitas vezes é conveniente filtrar apenas aquelas colunas de determinada classe (ou que satisfaçam determinada condição). A função Filter() é uma maneira rápida de fazer isso:
# seleciona apenas colunas numéricas Filter(is.numeric, funcionarios) ## salario experiencia ## 2 1200 12 ## 3 1300 15 # seleciona apenas colunas de texto Filter(is.character, funcionarios) ## nome sexo ## 2 Maria F ## 3 José M
Juntando filter() com sapply() você pode aplicar funções em apenas certas colunas, como por exemplo, calcular a média e máximo apenas nas colunas numéricas do nosso data.frame:
sapply(Filter(is.numeric, funcionarios), mean) ## salario experiencia ## 1250 14 sapply(Filter(is.numeric, funcionarios), max) ## salario experiencia ## 1300 15
Manipulando data.frames
Ainda temos muita coisa para falar de manipulação de data.framese isso merece um espaço especial. Veremos além de outras funções base do R alguns pacotes importantes como dplyr, reshape2 e tidyr em uma seção separada.

