***
Parte do livro Introdução à análise de dados com R. Este trabalho está em andamento, o texto é bastante preliminar e sofrerá muitas alterações.
Quer fazer sugestões? Deixe um comentário abaixo ou, se você sabe utilizar o github, acesse aqui.
Não copie ou reproduza este material sem autorização.
Volte para ver atualizações!
***
Distribuições de probabilidade
O R vem com diversas funções para simular distribuições estatísticas. Em geral essas funções têm o seguinte formato: rnomedadistribuicao, dnomedadistribuicao, pnomedadistribuicao ou qnomedadistribuicao. Mais detalhadamente, a primeira letra da função, que pode ser r, d, p ou q, indica, respectivamente, se a função é: (i) geradora de variáveis aleatórias; (ii) de densidade; (iii) de distribuição acumulada; ou, (iv) de quantil. E, logo em seguida, temos um nome abreviado da distribuição de probabilidade.
Dessa forma, por exemplo, se você quiser gerar dados aleatórios de uma distribuição normal a função para tanto é rnorm (r pois trata-se de um gerador de números aleatórios e norm pois trata-se da distribuição normal).
Na tabela abaixo temos várias das distribuições presentes de forma nativa no R:
Sementes para as simulações
Durante todo o livro nós utilizamos o comando set.seed quando fizemos simulações. Isso garante que os resultados obtidos possam ser reproduzidos em qualquer computador.
Veja que, se rodarmos o comando rnorm sem definir o estado do gerador de números aleatórios com set.seed, você não conseguirá obter os mesmos valores em seu computador:
rnorm(1) ## [1] 0.5748481 rnorm(1) ## [1] 0.4052027
Contudo, uma vez definida a semente, obteremos sempre o mesmo valor:
set.seed(1) rnorm(1) ## [1] -0.6264538 set.seed(1) rnorm(1) ## [1] -0.6264538
O básico de r,d p,q com a distribuição normal
Para começar a entender o que cada função do R faz, trabalhemos cada uma delas usando a distribuição normal. A função densidade da distribuição normal-padrão (uma normal com média zero e desvio-padrão igual a um) tem a seguinte forma:
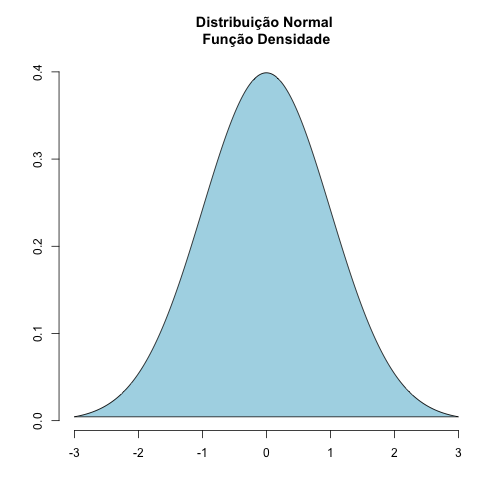
A primeira dúvida que alguém pode ter é: como extrair valores aleatoriamente desta distribuição? Vejamos:
# semente para reproducibilidade set.seed(2) # gerando 5 variáveis aleatórias da distribuição Normal(0,1) x1 <- rnorm(5) x1 ## [1] -0.89691455 0.18484918 1.58784533 -1.13037567 -0.08025176
Com o comando acima geramos 5 valores da normal-padrão.
Mas e se quisermos valores de uma normal com média e desvio-padrão diferentes? Para isso, basta mudarmos os parâmetros mean sd (standard deviation) da função rnorm:
# semente para reproducibilidade set.seed(2) # gerando 6 variáveis aleatórias da distribuição Normal(10,2) x2 <- rnorm(5, mean = 10, sd = 2) x2 ## [1] 8.206171 10.369698 13.175691 7.739249 9.839496
Com o código acima, geramos 5 valores de uma distribuição normal com média 10 e desvio-padrão 2. Entretanto, você também poderia ter gerado os mesmos valores a partir da normal-padrão: x2 nada mais é do que x1*2 + 10:
all.equal(x1*2 + 10, x2) ## [1] TRUE
Saber como tranformar uma distribuição em outra é algo bastante útil e pode poupar bastante tempo na hora de fazer simulações. Veremos exemplos práticos disso nos exercícios.
Às vezes, ao invés de gerar números aleatórios, nós temos valores que, presume-se, foram gerados por uma distribuição normal, e queremos saber a densidade ou a probabilidade associada àquele valor.
Por exemplo, supondo uma distribuição normal-padrão, qual a probabilidade de x ser menor do que 1.65? Isto é, queremos saber o valor da área hachurada da curva de densidade:
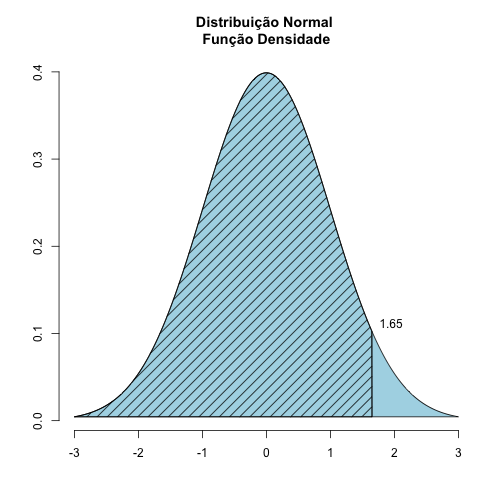
Para responder essa pergunta, você vai usar a função pnorm:
# probabilidade de X < 1.65 pnorm(1.65) ## [1] 0.9505285
Note que aproximadamente 95% dos valores da normal-padrão estão abaixo de 1.65. E se quisermos fazer a pergunta contrária: qual o valor de x tal que 95% dos valores da curva estejam abaixo deste valor? Para isso usamos a função qnorm:
qnorm(0.95) ## [1] 1.644854
Para calcularmos os valores da função densidade utilizamos a função dnorm. Vejamos como fazer isso reproduzindo os gráficos da função densidade exibidos anteriormente:
# Sequencia de -3 a 3 igualmente espaçada e # com valores redondos x <- pretty(c(-3, 3), 1000) # Função densidade de -3 a 3 y <- dnorm(x) # Gráfico Função Densidade plot.new() plot.window(xlim=range(x), ylim=range(y)) axis(1); axis(2) polygon(x, y, col = "lightblue") title(main = "Distribuição Normal \nFunção Densidade") # Gráfico Função Densidade Hachurado plot.new() plot.window(xlim=range(x), ylim=range(y)) axis(1);axis(2) polygon(x, y, col = "lightblue") title(main = "Distribuição Normal \nFunção Densidade") z <- 1.65 lines(c(z, z), y = c(dnorm(-3), dnorm(z))) polygon(c(x[x<=z], z), c(y[x<=z], min(y)), density = 10, angle = 45) text(x = z + 0.3, y = dnorm(z) + 0.01,"1.65")
Exemplo 1: Teorema Central do Limite
O teorema cental do limite nos diz que, sob certas condições de regularidade (como variância finita), quanto mais observações tivermos, a distribuição amostral da média de uma variável aleatória será aproximadamente normal, independentemente do formato original da distribuição.
Vejamos um exemplo com a distribuição exponencial. A função densidade da exponencial pode ser escrita como 
Para nosso exemplo, tomaremos 
Note que o formato do histograma da exponencial (
# semente para reproducibilidade set.seed(10) # geramos 1000 variávels aleatórias de uma distribuição exponencial x <- rexp(n = 1000, rate = 1) # histograma hist(x, col = "lightblue", main = "Distribuição Exponencial", freq = F)
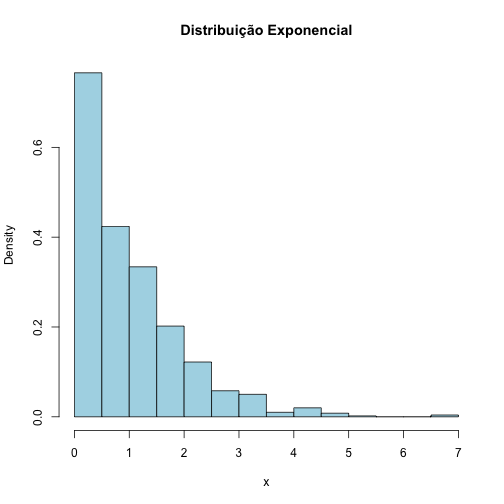
Entretanto, o que ocorre com a distribuição de 
# Simulacõees TCL - exponencial # semente para reproducibilidade set.seed(100) # diferentes tamanhos amostrais que iremos simular n <- c(1, 5, 10, 100, 500, 1000) # número de replicações para cada n n.rep <- 1000 ## simulações sims <- lapply(n, function(n) replicate(n.rep, (mean(rexp(n)) - 1)*sqrt(n)))
Na prática, a simulação toda foi feita com apenas uma linha, combinando o lapply com replicate. Explicando melhor o código acima, com o comando lapply(n, ...) estamos dizendo para o R que iremos aplicar uma função para cada valor de n. Mas que função estamos aplicando? Neste caso, a função anômima function(n) replicate(n.rep, (mean(rexp(n)) - 1)*sqrt(n)). Mais detalhadamente, com o comando replicate(n.rep, (mean(rexp(n)) - 1)*sqrt(n))) repetimos n.rep vezes a expressão (mean(rexp(n)) - 1)*sqrt(n)), que nada mais é do que a média padronizada de uma exponencial (n multiplicada por
O resultado de nossas simulações está na lista sims que tem a seguinte estrutura:
## nomes para as listas names(sims) <- as.character(n) ## estrutura do resultado str(sims) ## List of 6 ## $ 1 : num [1:1000] -0.0758 -0.2762 -0.8954 2.0974 -0.3752 ... ## $ 5 : num [1:1000] -0.25122 0.00986 -1.19437 -1.29553 1.14441 ... ## $ 10 : num [1:1000] -0.237 1.042 0.523 1.228 0.929 ... ## $ 100 : num [1:1000] -0.303 0.43 -0.25 -0.339 -0.659 ... ## $ 500 : num [1:1000] 2.072 0.239 -0.91 0.421 -0.353 ... ## $ 1000: num [1:1000] -1.0039 0.0282 -0.0259 -0.0925 -0.9421 ...
Perceba que temos uma lista com 6 elementos, um para cada n diferente. Você pode acessar os resultados da lista ou pelo índice ou pelo nome do elemento:
# pega os resultados de n = 1000 sims[[6]] sims[["1000"]]
Vejamos todos os resultados da simulação ao mesmo tempo em um gráfico. O histograma dos valores simulados estão em azul claro e a função densidade da normal-padrão em vermelho.
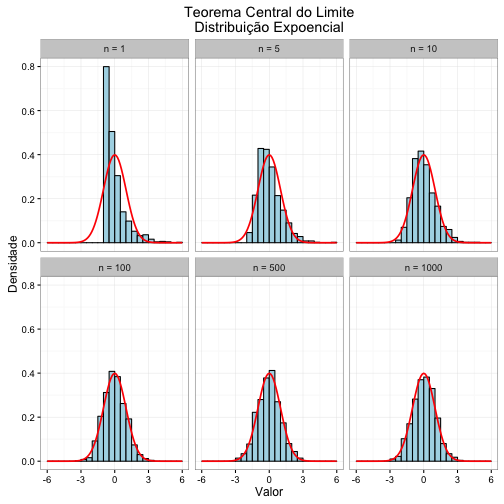
Quando n = 1, a distribuição segue o mesmo formato da exponencial. Todavia, note que a convergência para a distribuição normal ocorre bem rapidamente neste exemplo. Com n = 100 as diferenças entre a normal e os dados simulados já se tornam bastante pequenas.
Fizemos o gráfico acima com o ggplot2:
library(ggplot2)
library(reshape2)
# Prepara base de dados para gráfico
## Transforma em data.frame
sims.df <- as.data.frame(do.call("cbind", sims))
## Empilha para o ggplot2
sims.df <- melt(sims.df,
variable.name = "n",
value.name = "Valor")
sims.df$n <- paste("n =", sims.df$n)
sims.df$n <- factor(sims.df$n, levels = unique(sims.df$n))
# Histogramas vs Densidade Normal (ggplot2)
ggplot(sims.df, aes(x = Valor)) +
# Histograma
geom_histogram(aes(y = ..density..),
fill = "lightblue",
col = "black",
binwidth = 0.5) + xlim(c(-6, 6)) +
# Uma faceta para cada n
facet_wrap(~n) +
## Densidade da normal(0,1) para comparação
stat_function(fun = dnorm,
col = "red", size = 0.8) +
# Titulo principal e do eixo Y
ggtitle("Teorema Central do Limite\nDistribuição Expoencial") +
ylab("Densidade") +
## Tema em preto e branco
theme_bw()
Sua vez!
Nós simulamos o teorema central do limite usando funções da família apply: lapply e replicate. Isso permite nos expressarmos de maneira bastante concisa, em apenas uma linha.
Como você faria a mesma simulação usando loops? Compare os resultados e veja se eles são idênticos.
# Resposta sugerida
# Com FOR
## para reproducibilidade
set.seed(100)
## tamanho amostral
n <- c(1, 5, 10, 100, 500, 1000)
## numero de replicacoes
n.rep <- 1000
# lista para armazenar os resultados para cada n
sims.for <- vector("list", length(n))
## começo do for
## faremos n.rep replicacoes para cada n
## para cada i de n
for (i in seq_along(n)) {
# crie um vetor temporario para realizar n.rep repetições
temp <- numeric(n.rep)
# realiza n.rep repetições de (mean(rexp(n[i])) - 1)*sqrt(n[i])
for (j in 1:n.rep) {
temp[j] <- (mean(rexp(n[i])) - 1)*sqrt(n[i])
}
# guarda resultado na lista
sims.for[[i]] <- temp
}
# nomes para os resultados da lista
names(sims.for) <- n
# compara com simulação anterior
all.equal(sims, sims.for)
## [1] TRUE
Análise Real 