O maior encontro da comunidade do R, este ano, será na Universidade da California, em Los Angeles (UCLA), e desta vez estarei lá! Dêem uma olhada nos tutoriais programados – vai ser difícil escolher um. A UCLA também é a casa de dois excelentes pesquisadores que já mencionei aqui no blog: Edward Leamer e Judea Pearl – espero conseguir encontrá-los!
Metodologia
Aprenda a fazer previsão de eleições com o NYT.
Depois que o Nate Silver saiu do NYT, o jornal montou um novo time de previsão para eleições. O novo modelo, denominado LEO, está no ar e com uma descrição bem amigável de seu funcionamento. A parte gráfica dos resultados também está bacana, inclusive com uma seção comparando o modelo do NYT com seus concorrentes (vale lembrar que o site conta com a ajuda do Michael Bostock, um dos caras que desenvolveu o fantástico D3 para JavaScript)
Mas, tem algo ainda melhor. O NYT liberou os dados e os códigos do modelo no github. E o modelo é em R. Ou seja, agora, para replicar e adaptar o modelo à realidade brasileira só faltam duas coisas: tempo e vontade.
Que variáveis incluir na regressão? Ou, por que grande parte dos trabalhos aplicados está errada.
Suponha que você queira medir o efeito de X em Y (isto é, o quanto uma variação de X afeta Y – uma relação causal) e que você tenha mais duas variáveis que podem ser incluídas como controle, Z1 e Z2. Suponha ainda que você saiba que o modelo é linear, isto é, não há nenhuma incerteza com relação à especificação. Quais variáveis você incluiria no seu modelo?
Hoje, provavelmente você diria o seguinte: depende da significância! São Z1 e Z2 significantes? Se sim, eles devem ser incluídos.
Vejamos um exemplo de uma simulação. O código em R está ao final do post.
Vamos rodar as três regressões: uma só com X, outra incluindo Z1 e por fim uma com todos os controles. Os resultados foram os seguintes:
Equação 1: Y = -10 + 43X ***
Equação 2: Y = -7 + 13X * + 107Z1 ***
Equação 3: Y = -5 – 9X * + 46Z1 *** + 37Z2 ***
Pelos resultados, tanto Z1 quanto Z2 são significantes, então preferimos a equação 3. Concluímos que, na média, uma variação de 1 unidade de X reduz Y em 9 unidades. Certo?
***
Errado. O modelo ideal neste caso seria a equação 2. O efeito real de X sobre Y é de 10 (veja que valor estimado foi 13, bem próximo). O problema aqui é que a significância estatística não vai te responder sobre a pertinência de incluir ou não uma variável para estimar o efeito de X sobre Y. Infelizmente, não há almoço grátis. Como diz Judea Pearl, sem saber a estrutura do problema, não é possível determinar quais variáveis devem ser incluídas. Agora pense. Como é a lógica de trabalho dos artigos aplicados hoje? *** A simulação A nossa simulação tem a seguinte estrutura (U1 e U2 dizem respeito a duas variáveis não observadas, só observamos Y, X, Z1 e Z2):  O código em R para gerar os resultados é:
O código em R para gerar os resultados é:
gen_data <- function(N=200,s=2,beta1=10, beta2=100){
Z1 <- rnorm(N,0,s)
U2 <- rnorm(N,0,s) + Z1
U1 <- rnorm(N,0,s) + Z1
Z2 <- rnorm(N,0,s) + U2 + U1
X <- rnorm(N,0,s) + U1
Y <- rnorm(N,0,s) + beta1*X + beta2*U2
data.frame(Y,X,Z1,Z2)
}
set.seed(100)
data <- gen_data()
summary(lm(Y~X, data))
summary(lm(Y~X + Z1, data))
summary(lm(Y~X + Z1 + Z2, data))
Você pode brincar mais com o paradoxo de Simpson aqui; e o gráfico você pode fazer aqui.
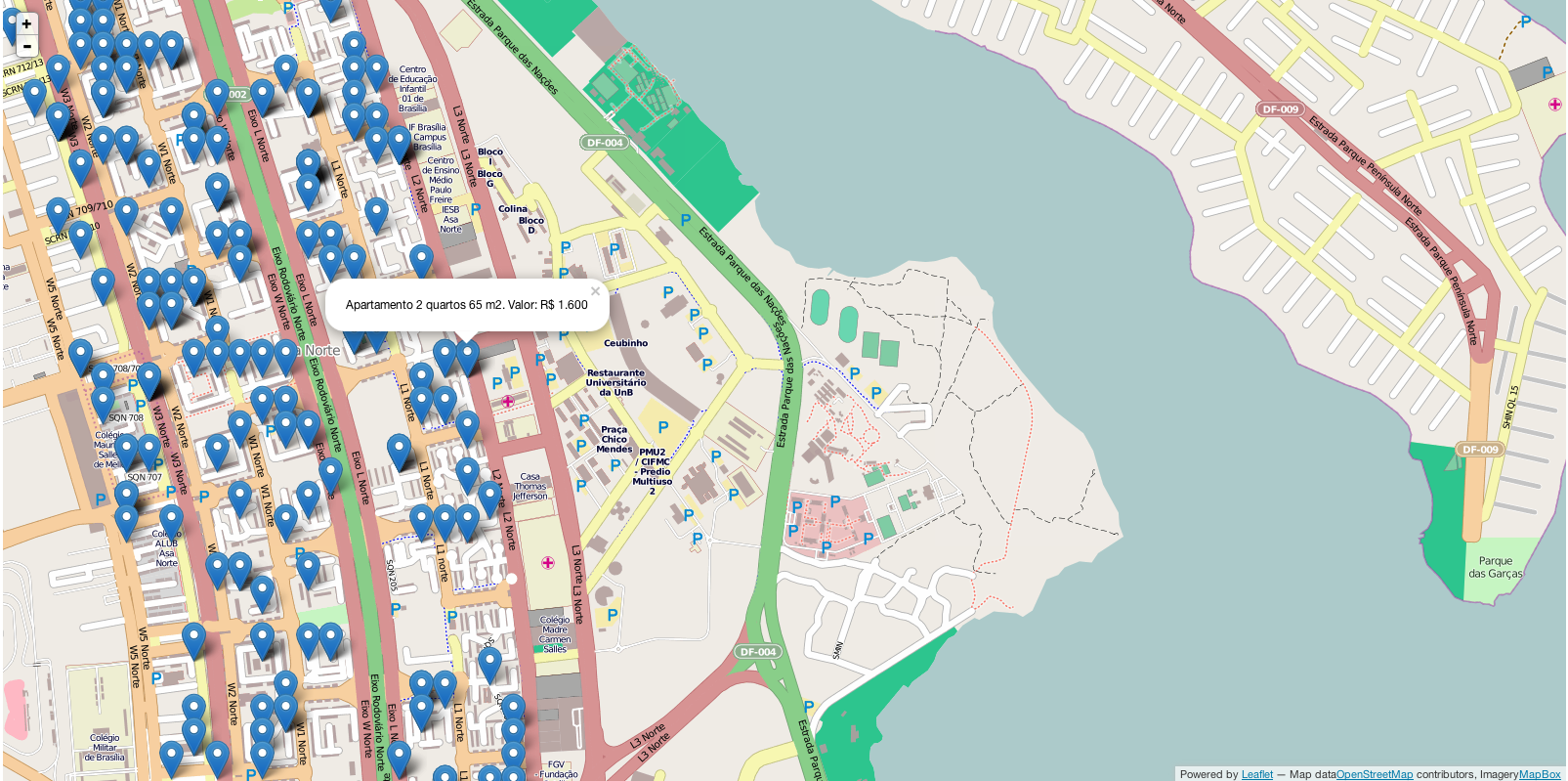
Mapa de aluguel em Brasília (Plano Piloto)
Em post anterior fizemos uma breve análise dos dados de aluguel no plano piloto.
Agora, que tal navegar por todos imóveis em um mapa da cidade, vendo a localização, tamanho, número de quartos e valor do aluguel? Clique aqui ou na mapa abaixo para navegar.
Atenção, ainda é um protótipo!
Se o mapa não aparecer na sua tela, provavelmente o seu navegador bloqueou a execução do javaScript. Procure por um cadeado no navegador (canto superior direito ou esquerdo, geralmente) e autorize o carregamento do site.
PS: agora já estamos coletando diariamente e automaticamente preços online de imóveis dos principais sites e das principais capitais do país. Ainda estamos testando métodos de análise e visualização.
Valores de aluguel em Brasília (plano piloto)
Está pesquisando apartamento para alugar em Brasília? Um pouco de web scraping, manipulação e visualização de dados com os valores (de oferta) dos aluguéis de 1.030 imóveis (Asa Sul, Asa Norte e Sudoeste) do site wimoveis pode ajudar a responder algumas perguntas interessantes.
A primeira delas: qual o bairro mais caro para se alugar, hoje, no plano piloto? Esta é uma pergunta que, veremos, depende do ponto de vista. Veja a tabela abaixo (versão ampliada aqui). M2 quer dizer metro quadrado e pm2 preço por metro quadrado.

Na média e mediana – em conformidade com a impressão pessoal de muitos – a Asa Sul é o bairro mais caro para se alugar dos três. Entretanto, note que isso ocorre porque há mais apartamentos maiores para aluguel na Asa Sul, e não porque o valor por metro quadrado é mais caro. Na verdade, o valor por metro quadrado, na média, é maior na Asa Norte e, na mediana, maior no Sudoeste.
Podemos agora decompor a tabela acima não somente por bairro, mas por bairro e número de quartos (versão ampliada aqui) . Na média, o bairro mais barato/caro para morar não é o mesmo a depender de quantos cômodos você quer no apartamento. E, uma curiosidade: na amostra, a média do tamanho dos apartamentos da Asa Norte, em todos os grupos de números de quartos, é menor do que a média do tamanho da Asa Sul.

Uma última forma de visualizar as diferenças de preços pode ser com um gráfico de densidade (versão ampliada aqui):

Veja que o pico do Sudoeste (em verde) é em valores mais altos do que na Asa Norte e na Asa Sul. Entretanto, a Asa Sul tem a “cauda” mais pesada em valores próximos a R$ 5.000.
Uma outra pergunta que podemos tentar responder é a seguinte: dos anúncios que temos hoje, na média, os preços daqueles atualizados em 2014 são maiores do que aqueles cuja última atualização foi feita em dezembro de 2013? Pelo quadro abaixo (versão ampliada aqui), infelizmente, sim, e por mais ou menos RS$100,00.

E como é a concentração da oferta dos anúncios por corretora? A distribuição de anúncios por imobiliária é homogênea?
Aparentemente, não. Veja o gráfico abaixo (versão ampliada aqui).
Enquanto algumas imobiliárias têm 30 a 40 apartamentos listados, muitas outras têm apenas 1 ou 5.
Isso quer dizer que os anúncios são concentrados? Não necessariamente. Note que apesar de a distribuição de anúncios não ser homogênea, a concorrência é bem grande, e usando como exemplo o índice de Herfindahl–Hirschman chegamos a um valor de 0.013, comumente considerado indicador de alta competitividade.
Há mais que poderíamos ver sobre aluguel. Mas deixemos para depois. No próximo (em algum próximo) post veremos os dados de valor de venda!
PS: iremos acompanhar regularmente esses preços. E não somente para Brasília. Uma área específica do blog será criada para isso.
Investimento Estrangeiro Direto no Brasil por Estado (Indústria)
Os dados do Censo de Capitais Estrangeiros no País, em 2010, trouxeram a distribuição do Investimento Estrangeiro Direto (IED) na indústria por Unidade da Federação (UF).
Somente da Indústria? E como foi feita a distribuição? Aqui voltamos ao que já dissemos sobre erro de medida (ver aqui, aqui, aqui e aqui, por exemplo). Distribuir o estoque investimento estrangeiro por UF é algo complicado, sujeito a erros diversos, tanto ao se definir a metodologia, quanto ao se mensurar o valor. No censo de 1995, por exemplo, os dados foram distribuídos por estado “[…] tomando por base o endereço da sede da empresa”. Será que essa é uma boa medida? Depende.
Percebe-se que uma indústria que concentre o grosso da sua estrutura produtiva no Pará, mas que tenha sede em São Paulo, será considerada um investimento nesta última UF. Se a intenção é medir onde se encontra o centro administrativo, esta medida poderá ser boa. Todavia, se intenção é medir onde se encontram as unidades produtivas, esta medida terá, talvez, distorções significativas. Qual a melhor forma, então, de se distribuírem os investimentos por estado? Pela localização da sede? Pela localização do ativo imobilizado? Pela distribuição dos funcionários? Particularmente, acho que não existe uma métrica única que se sobressaia às demais – a melhor opção depende do uso que você irá fazer da estatística.
Voltando ao Censo, a pesquisa passou a considerar a distribuição do ativo imobilizado como critério para alocação do IED – e apenas para a indústria . Os declarantes distribuíram percentualmente o seu imobilizado pelos diferentes estados e isso foi utilizado para ponderar o investimento direto pelas UF’s.
Segue abaixo mapa do Brasil com a distribuição do IED da indústria por Unidade Federativa:
Para aprender a fazer o mapa, veja aqui.
Você é obeso… mas não é gordo 2! Ou, mais sobre p-valores.
Já falamos que os p-valores não podem ser interpretados como uma medida absoluta de evidência, como comumente costumam ser. Entre algumas interpretações recorrentes, por exemplo, vale mencionar alguns cuidados:
- se para um certo conjunto de dados, uma hipótese A (e uma estatística calculada sob A) gera um p-valor de 1% e outra hipótese B (e uma estatística calculada sob B) gera um p-valor de 10%, isto não necessariamente quer dizer que os dados trazem mais evidência contra A do que contra B. Até porque rejeitar A pode implicar, logicamente, na rejeição de B.
- se para um certo conjunto de dados, uma hipótese A (e uma estatística calculada sob A) gera um p-valor menor que 5%, isto não necessariamente é evidência contra A.
- se um estudo sobre a hipótese A resulta em p-valor menor do que 5% e outro estudo gera um p-valor maior do que 5%, isto não necessariamente quer dizer que os estudos apresentam resultados contraditórios.
Dentre outras questões.
Mas o que essas coisas querem realmente dizer? Muitas vezes é difícil entender o conceito sem exemplos (e gráficos) e é isso que pretendemos trazer hoje aqui. Vamos tratar do primeiro ponto listado, uma questão que, muitas vezes, pode confundir o usuário do p-valor: o p-valor pode apresentar evidências de que alguém seja obeso e, ao mesmo tempo, evidências de que este alguém não seja gordo, caso você, por descuido, tome o p-valor como uma medida absoluta de evidência e leve suas hipóteses nulas ao pé da letra. O exemplo abaixo foi retirado do artigo do Alexandre Patriota (versão publicada aqui).
Considere duas amostras aleatórias, com 100 observações cada, de distribuição normal com médias desconhecidas e variância igual 1. Suponha que as médias amostrais calculadas nas duas amostras tenham sido x1=0.14 e x2=-0.16 e que você queira testar a hipótese nula de que ambas as médias populacionais sejam iguais a zero.
A estatística para esta hipótese é n*(x1^2+x2^2), e o valor obtido na amostra é 100*(0.14^2+(-0.16)^2)=4.52. A distribuição desta estatística, sob a hipótese nula, é uma qui-quadrado com 2 graus de liberdade, o que te dá um p-valor de 10%. Assim, se você segue o padrão da literatura aplicada, como o p-valor é maior do que 5%, você dirá que aceita (ou que não rejeita) a hipótese nula de que as médias sejam iguais a zero.
Agora suponha que outro pesquisador teste, com os mesmos dados, a hipótese de que as médias populacionas sejam iguais a si. Para esta hipótese, a estatística seria (n/2)*(x1 – x2)^2, e o valor obtido na amostra é (100/2)*(0.14+0.16)^2= 4.5. A distribuição desta estatística sob a hipótese nula é uma qui-quadrado com 1 grau de liberdade, o que te dá um p-valor de 3%. Caso o pesquisador siga o padrão da literatura aplicada, como o p-valor é menor do que 5% (o tão esperado *), ele dirá que rejeita a hipótese de que as médias sejam iguais.
Mas, espere um momento. Ao concluir que as médias não são iguais, logicamente também se deve concluir que ambas não sejam iguais a zero! Com os mesmos dados, se forem testadas hipóteses diferentes, e se os resultados forem interpretados conforme faz a maior parte da literatura aplicada (que é uma interpretação bastante frágil), você chegará a conclusões aparentemente contraditórias!
Como o p-valor traz “mais evidência” contra a hipótese de que as médias seja iguais do que contra a hipótese de que ambas sejam iguais a zero, tendo em vista que se rejeitarmos a primeira, logicamente temos que rejeitar a segunda? O que está acontecendo?
Para entender melhor, lembremos o que é o p-valor. O p-valor calcula a probabilidade de a estatística de teste ser tão grande, ou maior, do que a estatística de teste observada. Intuitivamente, o p-valor tenta responder a seguinte pergunta: se eu adotasse esta discrepância observada como evidência suficiente para rejeitar a hipótese nula, quantas vezes este teste me levaria a erroneamente rejeitar esta hipótese quando ela é de fato verdadeira. Isto é, o p-valor leva em consideração em seu cálculo todos aqueles resultados amostrais que gerariam estatísticas tão extremas quanto a observada, que poderiam ter ocorrido mas não ocorreram.
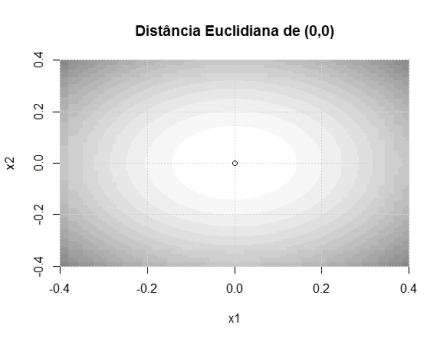
Repare como calculamos a estatística 1 e note o termo (x1^2+x2^2). Percebe-se que a estatística se torna mais extrema cada vez que o ponto (x1, x2) se distancia de (0,0) – em qualquer direção. Isto é, ela cresce com relação à distância euclidiana de (x1,x2) em relação ao ponto (0,0). Talvez isso seja mais fácil de entender com imagens. No gráfico abaixo, quanto mais escura a cor, maior é o valor da estatística de teste.
Já na estatística 2, perceba que o termo principal é (x1 – x2)^2, e o que se mede é a distância do ponto em relação à curva x1=x2. Isto é, a distância absoluta de x1 em relação a x2. Vejamos as curvas de nível. Note que ao longo da curva há diversas regiões em branco, mesmo quando distantes do ponto (0,0), pois o que a estatística mede é a distância entre os pontos x1 e x2 entre si.
Agora deve ficar mais fácil de entender o que está acontecendo. O p-valor calcula a probabilidade de encontrar uma estatística tão grande ou maior do que a observada. Ao calcular (x1 – x2)^2, todos os pontos que são distantes de (0,0), mas são próximos entre si, não geram estatísticas extremas. Como uma imagem vale mais do que mil palavras, façamos mais uma. No gráfico abaixo, os pontos pretos são todos aqueles cuja estatística de teste supera a estatística observada (0.14, -0.16). Já os pontos azuis e vermelhos são todos os pontos que tem uma estatística de teste maior do que a observada, medidos pela distância euclidiana em relação à reta x1=x2.
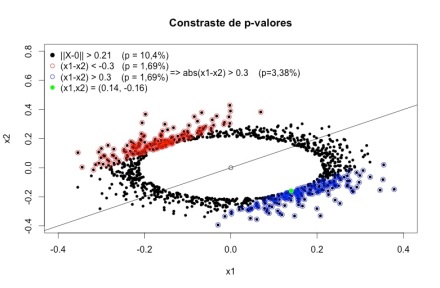 Note que vários pontos pretos que se encontram “longe” de (0,0) não são nem vermelhos nem azuis, pois estão “pertos” da reta x1=x2. Fica claro, portanto, porque o p-valor da segunda estatística é menor. Isso ocorre porque resultados extremos que discordariam bastante de (0,0) – como (0.2, 0.2) ou (0.3, 0.3) – não são considerados em seu cálculo. Note que é possível obter um p-valor ainda menor (1,6%) testanto a hipóse de que média 1 seja menor ou igual à média 2. E se a média 1 não é menor ou igual a média 2, isso implica que elas não são iguais a si, e que também não são ambas iguais a zero. É importante ter claro também que todas as estatísticas são derivadas pelo mesmo método – razão de verossimilhanças – e possuem propriedades ótimas, não são estatísticas geradas ad-hoc para provocar um resultado contra-intutivo.
Note que vários pontos pretos que se encontram “longe” de (0,0) não são nem vermelhos nem azuis, pois estão “pertos” da reta x1=x2. Fica claro, portanto, porque o p-valor da segunda estatística é menor. Isso ocorre porque resultados extremos que discordariam bastante de (0,0) – como (0.2, 0.2) ou (0.3, 0.3) – não são considerados em seu cálculo. Note que é possível obter um p-valor ainda menor (1,6%) testanto a hipóse de que média 1 seja menor ou igual à média 2. E se a média 1 não é menor ou igual a média 2, isso implica que elas não são iguais a si, e que também não são ambas iguais a zero. É importante ter claro também que todas as estatísticas são derivadas pelo mesmo método – razão de verossimilhanças – e possuem propriedades ótimas, não são estatísticas geradas ad-hoc para provocar um resultado contra-intutivo.
Para não alongar muito este post, frise-se que o que deve ser tirado como lição principal é que o p-valor não é uma medida absoluta de suporte à hipótese que está sendo testada. Mas como interpretar melhor os resultados acima? Caso você queira continuar no âmbito frequentista, algumas medidas seriam, por exemplo, não considerar literalmente as hipóteses nulas (isto é, não rejeitar ou aceitar uma hipótese precisa como x1=x2 ou x1=x2=0), avaliar que discrepâncias em relação à hipótese nula são ou não relevantes (do ponto de vista científico, e não estatístico) e conferir a função poder e intervalos de confiança para algumas alternativas de interesse. Trataremos disso mais a frente (caso vocês ainda não tenham enjoado do assunto!).
Voltando ao caso da Target: previsão de gravidez
Lembra da história da Target prevendo quando uma cliente terá um bebê? Veja aqui vídeo de Andrew Pole, da Target, falando sobre o uso de dados para melhorar o marketing da empresa. Entre os exemplos, ele cita o famoso caso de prever a gravidez (para ir diretamente à parte dos exemplos clique, em cima do video, em “Data to Drive Performance Examples”).
Solucionando crimes com matemática e estatística
Enquanto Breaking Bad não volta, comecei a assistir ao seriado Numb3rs, cujo enredo trata do uso da matemática e da estatística na solução de crimes. Confesso que, a princípio, estava receoso. Na maior parte das vezes, filmes e seriados que tratam desses temas costumam, ou mistificar a matemática, ou conter erros crassos.
Todavia, o primeiro episódio da série abordou uma equação para tentar identificar a provável residência de um criminoso, sendo que: (i) os diálogos dos personagens e as explicações faziam sentido; e, algo mais surpreendente, (ii) as equações de background, apesar de não explicadas, pareciam fazer sentido. Desconfiei. Será que era baseado em um caso real?
E era. Bastou pesquisar um pouco no Google para encontrar a história do policial que virou criminologista, Kim Rossmo, em que o episódio foi baseado. E inclusive, encontrar também um livro para leigos, de leitura agradável, que aborda alguns dos temas de matemática por trás do seriado: The Numbers behind Numb3rs.
A primeira equação que Rossmo criou tinha a seguinte cara:
A intuição por trás da equação pode ser resumida desta forma: o criminoso não gosta de cometer crimes perto da própria residência, pois isso tornaria muito fácil sua identificação; assim, dentro de uma certa zona B, a probabilidade de o criminoso residir em um certo local é menor quanto mais próximo este estiver do crime (esse é o segundo termo da equação). Entretanto, a partir de certo ponto, começa a ser custoso ao criminoso ir mais longe para cometer o crime – assim, a partir dali, a situação se inverte, e locais longe do crime passam a ser menos prováveis (esse é o primeiro termo da equação). Em outras palavras, você tenta calcular a probabilidade de um criminoso morar na coordenada (Xi , Xj), com base na distância desta com as demais coordenadas dos crimes (xn, yn), levando em conta o fato de a residência estar ou não em B. Os parâmetros da equação são estimados de modo a otimizar o modelo com base nos dados de casos passados.
Por mais simples que seja, a equação funcionou muito bem e Kim Rossmo prosseguiu com seus estudos em criminologia. Evidentemente que, como em qualquer modelo, há casos em que a equação falha miseravelmente, como em situações em que os criminosos mudam de residência o tempo inteiro – mas isso não é um problema da equação em si, pois o trabalho de quem a utiliza é justamente identificar se a situação é, ou não, adequada para tanto. Acho que este exemplo ilustra muito bem como sacadas simples e bem aplicadas podem ser muito poderosas!
PS: O tema me interessou bastante e o livro de Rossmo, Geographic Profiling, entrou para a (crescente) wishlist da Amazon.
Dificuldades metodológicas na coleta de dados
Como já havia citado antes, segundo Leontief, o economista é famoso por não sujar as mãos coletando os próprios dados. Ao não colocar a mão na massa, acaba sendo fácil não se familiarizar com os detalhes e a acurácia dos dados que utiliza. E, muitas vezes, os detalhes do processo revelam dificuldades que você sequer imagina. Vejam, abaixo, alguns problemas de coleta de dados enfrentados pelo IBGE, na Pnad!
Imagens da apresentação do 12º Fórum Sistema Integrado de Pesquisas Domiciliares (slides 54 a 72).
Dica do Ricardo Sabbadini