Compartilharam, recentemente, uma análise das eleições presidenciais utilizando a lei de Benford. Para quem não conhece, a lei de Benford é bastante utilizada na detecção de fraudes em uma gama de circunstâncias, como demonstrações contábeis e, inclusive, eleições. Para entender um pouco mais sobre o assunto, leia aqui (Lei de Benford), aqui (Lei de Benford – por que ela surge?) ou aqui (benford.analysis 0.1).
A análise tomou os votos da Dilma por município e extraiu os primeiros dígitos das observações. Por exemplo, se em um dado município foram contabilizados 1.529 votos para a candidata, o primeiro dígito é 1. Já se o número tivesse sido 987, o primeiro dígito é 9. Segundo a lei de Benford, deveríamos observar cerca de 30,1% dos municípios começando com o dígito 1; em seguida, 17,6% dos municípios com a totalização dos votos iniciada pelo número 2. E assim sucessivamente, como no gráfico a seguir:

Se os números observados diferirem substancialmente do que é previsto pela lei, isso poderia ser um indício de manipulação dos dados ou de algum outro fato atípico. Mas, seria pertinente utilizar este instrumento para analisar fraudes em votos municipais? Para responder a essa pergunta, devemos responder, na verdade, outra: estes dados tenderiam a ter uma distribuição de Benford?
Em uma primeira aproximação, a resposta é sim. Dados de população municipal tendem a seguir a lei de Benford. Veja, por exemplo, a distribuição dos primeiros dígitos dos dados de população por município, no Brasil (estou utilizando o pacote de R benford.analysis; o gráfico em que você tem que prestar mais atenção é o primeiro, em que a linha pontilhada vermelha é o valor previsto e a barra azul é o valor observado):
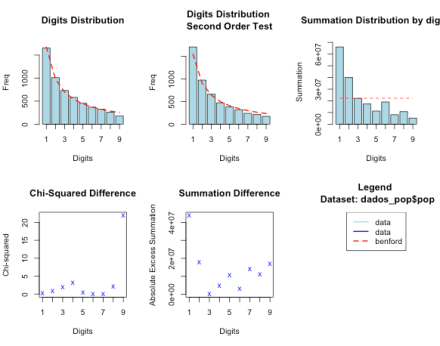
Ora, e como a população define o eleitorado, também é de se esperar que a lei tenda a aparecer nos números de eleitores. E, de fato, aparece:

E, por fim, como o eleitorado define o número de votos dos candidatos, também é natural se esperar que a distribuição apareça nesta situação. Em todos os casos vale lembrar que a lei de Benford nunca valerá exatamente, será apenas uma aproximação – testes estatísticos formais tem que ser interpretados com cautela e não são muito úteis, a principal função da lei é identificar possíveis focos de observações que mereçam análise/auditoria mais aprofundada.
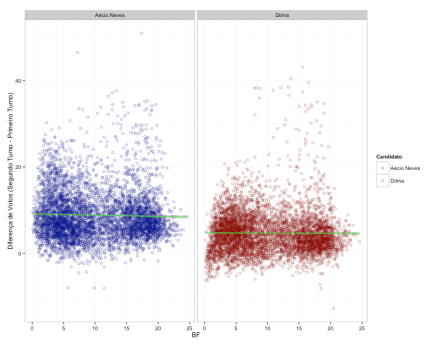
Voltando, portanto, à análise mencionada anteriormente, foram calculados os desvios dos valores observados em relação aos valores esperados e, com isso, a estatística de chi-quadrado. Mas isso foi feito para cada estado da federação:

Note que alguns estados em que Dilma ganhou com bastante diferença como BA, PE ou PI tem grande discrepância em relação ao esperado pela lei, e isso causou certa estranheza. Por que logo estes estados?
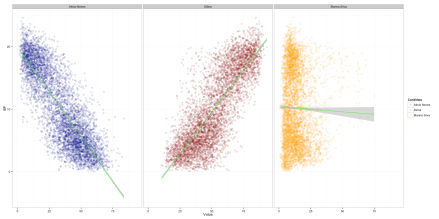
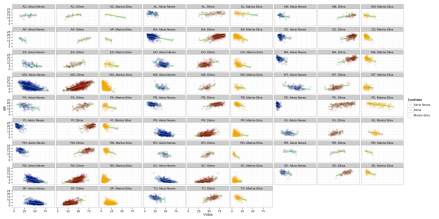
Contudo, ocorre que, apesar de a distribuição do número de eleitores (ou da população) por municípios ter um bom ajuste quando usamos os dados do Brasil inteiro, isso não precisa valer para cada estado separadamente. E de fato não vale. Para deixar mais claro, vejamos, abaixo, o grau de ajuste do número de eleitores e da população para cada estado separadamente, e comparemos isso com o ajuste do número de votos:

Note que a Bahia tem um chi-quadrado alto para o número de votos (72.725), mas também já tinha esse valor alto para o número de eleitores (68.988) e população (60.712). Observa-se a mesma coisa com MG, PE, PI e RS, por exemplo. Na verdade, a correlação dessas três séries é bem alta. A correlação entre o Qui-Quadrado do número de votos e o Qui-Quadrado do Número de Eleitores é de 0.968.

Deste modo, para o caso em questão, as grandes discrepâncias entre a lei de Benford e o número de votos em alguns estados parecem decorrer, em grande medida, do próprio desvio já presente nas distribuições da população e do eleitorado.
Há mais coisas que podem ser investigadas nos dados, e acho que esse é um bom exemplo para explorar a lei de Benford na prática. Por exemplo, a lei de Benford não estipula somente uma distribuição para o primeiro dígito, mas sim para todos os dígitos significativos, então você poderia analisar os dois primeiros dígitos (dada a quantidade de observações, não acredito que dê para analisar os três primeiros). Ou, ainda, verificar se a divisão por regiões mais amplas do país tenderiam a seguir a lei para o eleitorado (e para o número de votos).
Para replicar os cálculos acima, você pode utilizar estes dados aqui (link) e o script de R a seguir:
# instale o pacote e carregue os dados
install.packages("benford.analysis")
library(benford.analysis)
load("benford_eleicoes.rda")
#### Geral ####
bfd_votos <- benford(votos_dilma$votos, number.of.digits=1)
plot(bfd_votos)
bfd_pop <- benford(dados_pop$pop, number.of.digits=1)
plot(bfd_pop)
bfd_eleitorado <- benford(eleitorado$eleitores, number.of.digits=1)
plot(bfd_eleitorado)
#### Por Estado ####
# separando os dados
split_votos_uf <- split(votos_dilma, votos_dilma$uf)
split_pop_uf <- split(dados_pop, dados_pop$uf)
split_eleitorado_uf <- split(eleitorado, eleitorado$uf)
# benford dos votos
bfd_votos_uf <- lapply(split_votos_uf, function(x) benford(x$votos, number.of.digits=1))
chi_votos_uf <- sapply(bfd_votos_uf, function(x) chisq(x)$stat)
chi_votos_uf
# plote um estado de exemplo
plot(bfd_votos_uf[["BA"]])
# benford da população
bfd_pop_uf <- lapply(split_pop_uf, function(x) benford(x$pop, number.of.digits=1))
chi_pop_uf <- sapply(bfd_pop_uf, function(x) chisq(x)$stat)
chi_pop_uf
# plote um estado de exemplo
plot(bfd_pop_uf[["BA"]])
# benford do eleitorado
bfd_eleitorado_uf <- lapply(split_eleitorado_uf, function(x) benford(x$eleitores, number.of.digits=1))
chi_eleitorado_uf <- sapply(bfd_eleitorado_uf, function(x) chisq(x)$stat)
chi_eleitorado_uf
# plote um estado de exemplo
plot(bfd_eleitorado_uf[["BA"]])
# comparando as estatísticas chi-quadrado
compara <- data.frame( Chi_Quadrado_Votos = chi_votos_uf,
Chi_Quadrado_Número_de_Eleitores = chi_eleitorado_uf,
Chi_Quadrado_População = chi_pop_uf)
row.names(compara) <- gsub("([A-Z]{2}).*", "\\1", row.names(compara))
compara
# correlações
cor(compara)